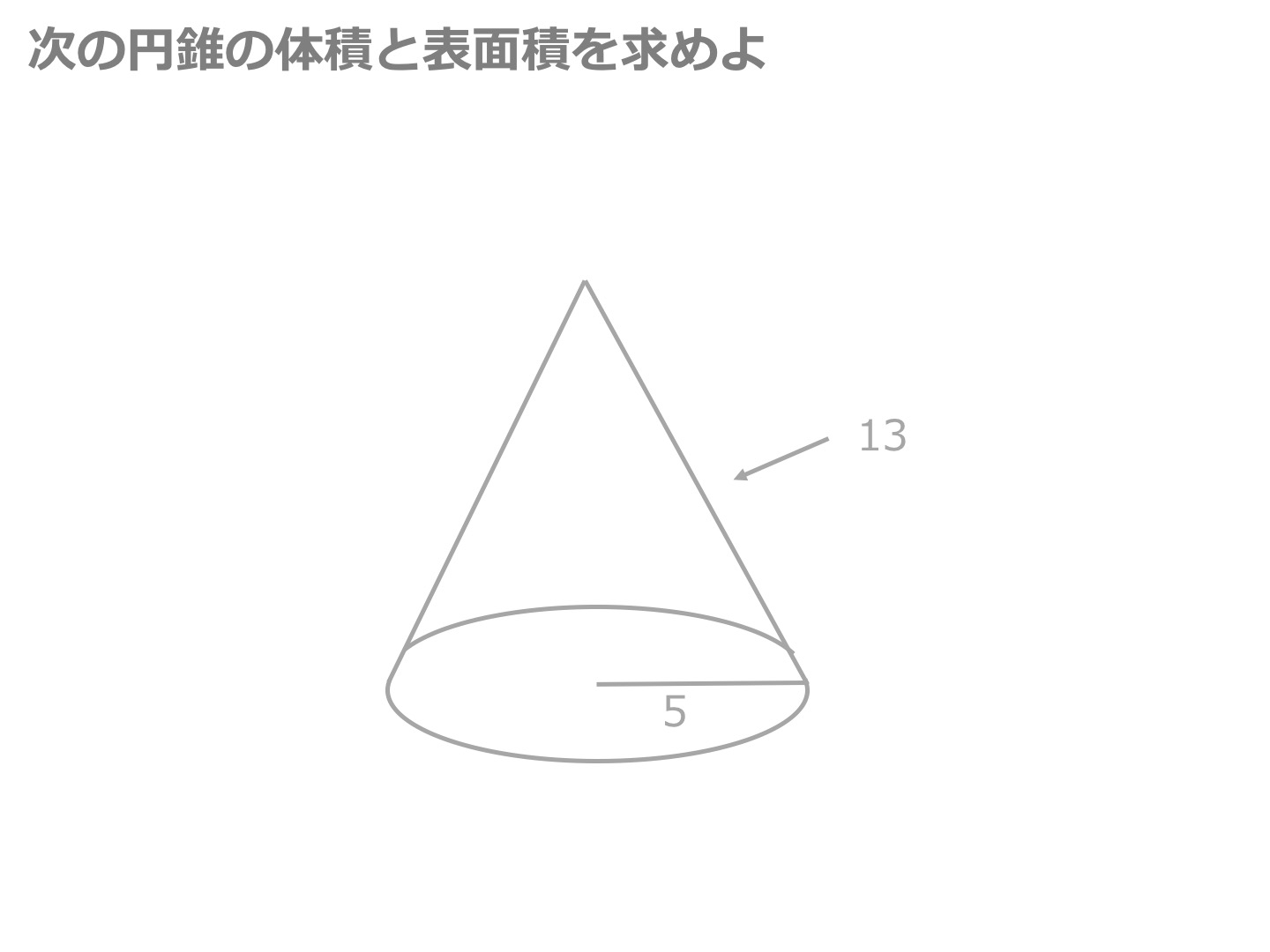
体積や表面積を求める問題はよく目にすると思いますが その中でも円錐を取り上げた問題が一番よく出題されます。 なぜなら、円錐の問題には 空間図形の知識だけでなく、おうぎ形の知識も一緒に問うことができるからです。5:円錐の表面積に関する練習問題 最後は円錐の表面積に関する練習問題です。 問題1 底面の円の半径が5、母線が13の円錐があるとき、この円錐の体積・表面積をそれぞれ求めよ。、g とします。このとき 次の図形の面積比を求めなさい。 (1) adf: abc (2) 四角形degf:四角形ebcg 2 右の図の abcd で、辺 ad 上に点e を ae :ed=2:1 になるようにとり、bd と ec の交点を f とします。 efd=6cm2 のとき、次の図形の面積を求めなさい。 (1) cfb (2)

立体の表面積 無料で使える中学学習プリント
円錐 表面積 問題
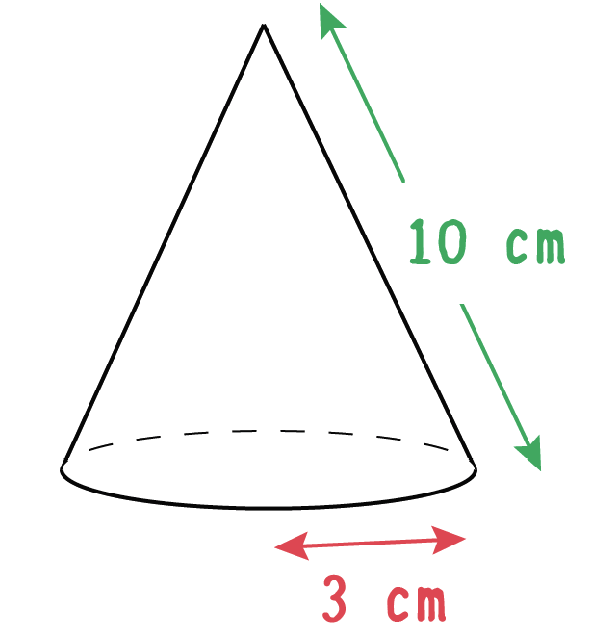
円錐 表面積 問題-7 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。おうぎ形の面積 = 円の面積× a 360 より 側面のおうぎ形の面積 = 10×10×π× 108 360 = 30π 底面の円の面積 = 3×3×π =9π




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題
Hello School 算数 体積・表面積 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※特に指定がない場合、円周率は314とします。空間図形 練習問題 空間図形1 空間図形2 表面積 体積1 体積2 体積3 (発展) 体積4 (発展) 空間図形 (発展) (1)①10π ②12 表面積 170πcm 2 (2)①12 ②8π 表面積 64πcm 2 (1) 280 cm 2 (2) 104πcm 2 (3) 510 cm 2 (1) 39πcm 2円すいの側面積は、半径が母線のおうぎ形なので、 側面積 = 母線×母線×π× x 360 側 面 積 = 母 線 × 母 線 × π × x 360 ですが、 x 360 = 底面の半径 母線 x 360 = 底 面 の 半 径 母 線 でしたので、これを代入すると、 側面積= 母線×母線×π× x 360 側 面 積 = 母 線 × 母 線 × π × x 360 =母線×母線×π× 底面の半径 母線 = 母 線 × 母 線 × π × 底 面 の 半 径 母 線 =母線×π×
練習1: 四角錐と円錐があります。 ①四角錐の表面積は何 ですか。 ②円錐の表面積は何 ですか。 この問題の説明 錐の表面積を求める公式は覚えているッピか? 忘れてしまった人はしっかり確認しましょう。 面積や体積を求める公式は、ひたすら 側面積=母線×半径×π =9×3×π =27π (㎠) 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積を 円錐の体積=底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク 円錐の体積を求める問題 // では、実際に円錐の体積を求める問題を解いていきたいと思います。
問題(3 学期) 次のような立体を,下の の中からすべて選べ。 ① 平面と曲面で囲まれた立体 ② 1 つの四角形と4 つの三角形で囲まれた立体 直方体 円錐 三角錐 四角錐 円柱 三角柱 解答欄 ①面積が円錐の表面積から底面の面積を引けば出るので 60π25π =35πcm2 弧の長さは底面の周と等しいので 10πcm 10π 35π x おうぎ形の面積 = おうぎ形の半径×弧÷2より おうぎ形の半径をxとすると 35π = x × 10π ÷2 x = 7 側面のおうぎ形の半径は母線の長さに側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる
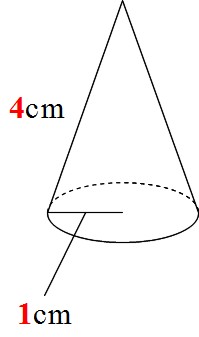



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




公式を図解 すい体の体積 円すいの表面積の求め方
Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ご右図イの四角柱の表面積 底面:3×4=12(cm 2)の長方形が2つ 側面:5×4=(cm 2)の長方形が2つ 側面:5×3=15(cm 2)の長方形が2つ 計94(cm 2)・・・答 図ウの円柱の表面積 ウ 底面: π ×2 2 =4 π (cm 2)の円が2つ 側面:底面の円周の長さと側面の横の長さが等しいから 5×4 π = π (cm 2)の長方 問題 今回の問題はこちら 底面積を求める 底面積は、円の面積を求めるだけだね 忘れちゃった人は、円の面積を直径から求める図付きを見てみてね。 円の面積のおもしろ問題3選!美味しそうな色合いこれも面白いよ 底面積は、公式を使って



1



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor
②この円柱の表面積を求めなさい。 2.底面の半径が ㎝で,母線の長さが ㎝の円錐があります。 ( )cm cm →展開図 5cm cm ①上の図で底面の円周の長さを求めなさい。 ②上の図で側面の中心角を求めなさい。 ③側面積を求めなさい。 ④表面積を求めなさい 練習問題2 練習問題1の円柱の表面積を求めよ。 練習問題2の解答・解説 表面積も上で説明した通り、1つずつやります。 底面積は、練習問題1で求めたように \(4π\) です。 表面積を求める場合、円柱の底と蓋に底面積があるので、2倍して\(8π\)となります。空間図形 円錐の表面積 円錐の表面積=(底面積)+(側面積) 底面積はただの円ですから簡単です。 問題は側面積。 側面積を求めるために中心角を出そうとするのは、あまり良い手ではありません。 別の公式を使いましょう。



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com
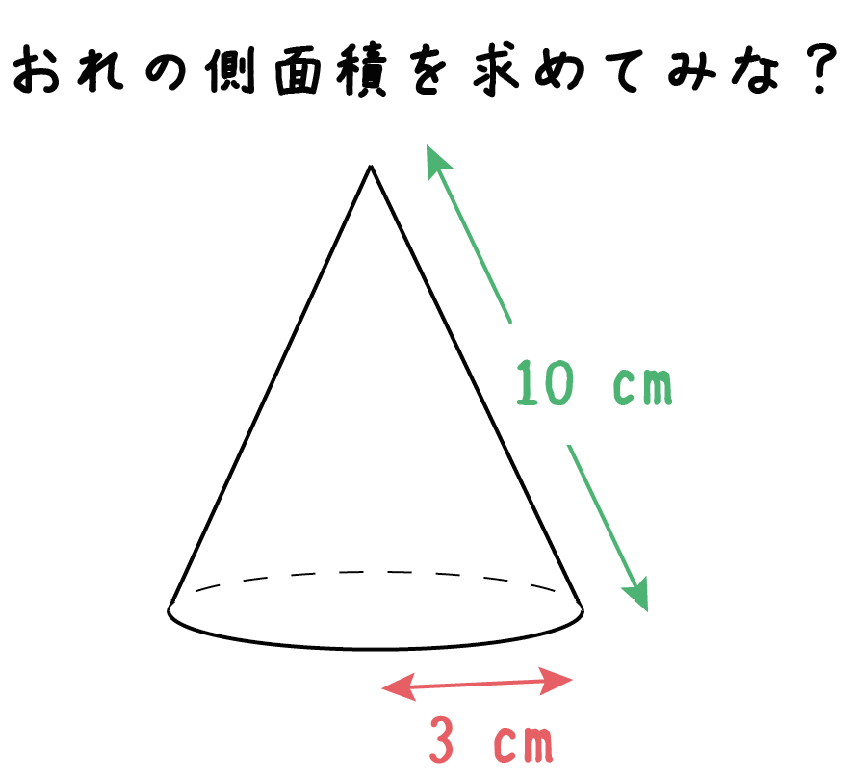



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
前述の通り、円錐の表面積 S を求める公式は、次の通りです。 S = πr(r R) = π ×(底面の半径)× {(底面の半径) (母線の長さ)} S = π r (r R) = π × (底面の半径) × { (底面の半径) (母線円すいの表面積 次の図形の表面積を求めましょう。 問題集の無料ダウンロードサイトは「おかわりドリル」で検索 https//wwwokadorinet ©おかわりドリル ① 2cm 4cm 5cm 4cm ② ③ 6cm 4cm 1cm 底面積は2×2×π=4π 側面のおうぎ形の弧の長さは2×2×π=4π 側面積は1/2×4πいろいろな立体の問題 第5節 円柱と円錐(その3) 以前,円錐から平面で切り取った立体についての次の問題を扱いました.
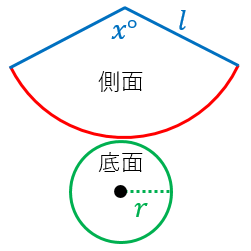



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



円錐とは 体積 表面積の公式や求め方 受験辞典
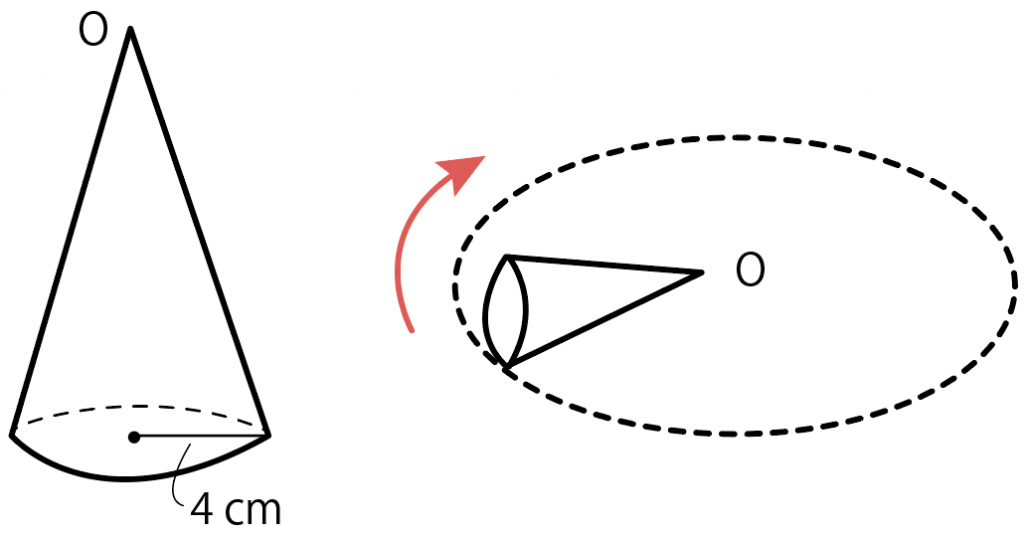
よって、表面積は $15π9π=\textcolor{red}{24π\rm cm^2}$ 母線の長さ 問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中1数学 円すいの体積 表面積の求め方と練習問題 Examee
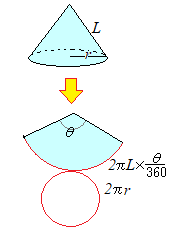



立体の表面積




立体の表面積 無料で使える中学学習プリント




公式を図解 すい体の体積 円すいの表面積の求め方



中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル



5ステップでわかる 円錐が滑らずに転がる問題の解き方 Qikeru 学びを楽しくわかりやすく




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




円錐の表面積 Youtube



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3分でわかる 円錐の体積 表面積の求め方 合格サプリ



Math 横にした円錐が転がる問題 中学生 働きアリ




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題
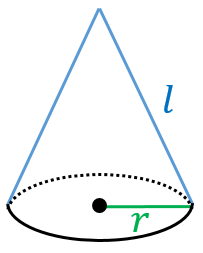



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




立体の表面積 無料で使える中学学習プリント




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
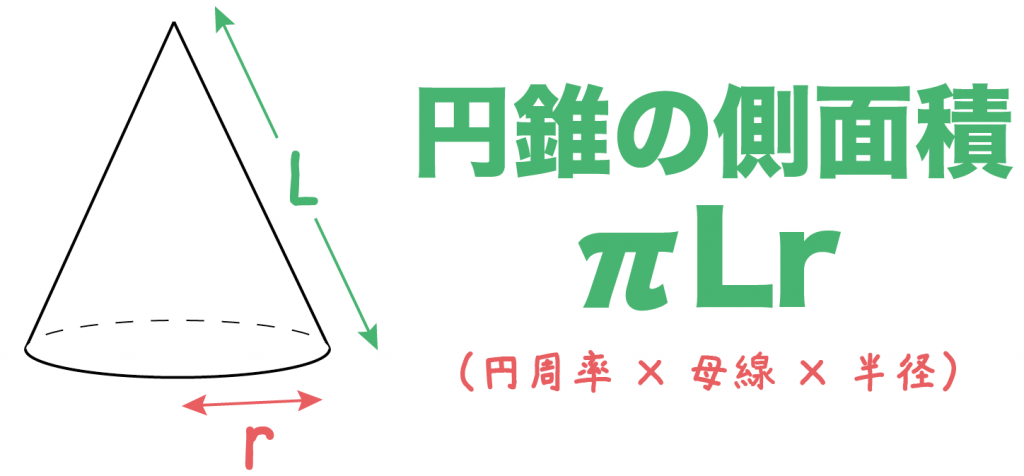



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積を 中心角を使って求める チーム エン




円錐表面積を2秒で出す公式 中学生 数学のノート Clear




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




高校入試対策数学 円錐に関する対策問題 Pikuu




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積 あんず学習塾のメモ 図表置き場




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
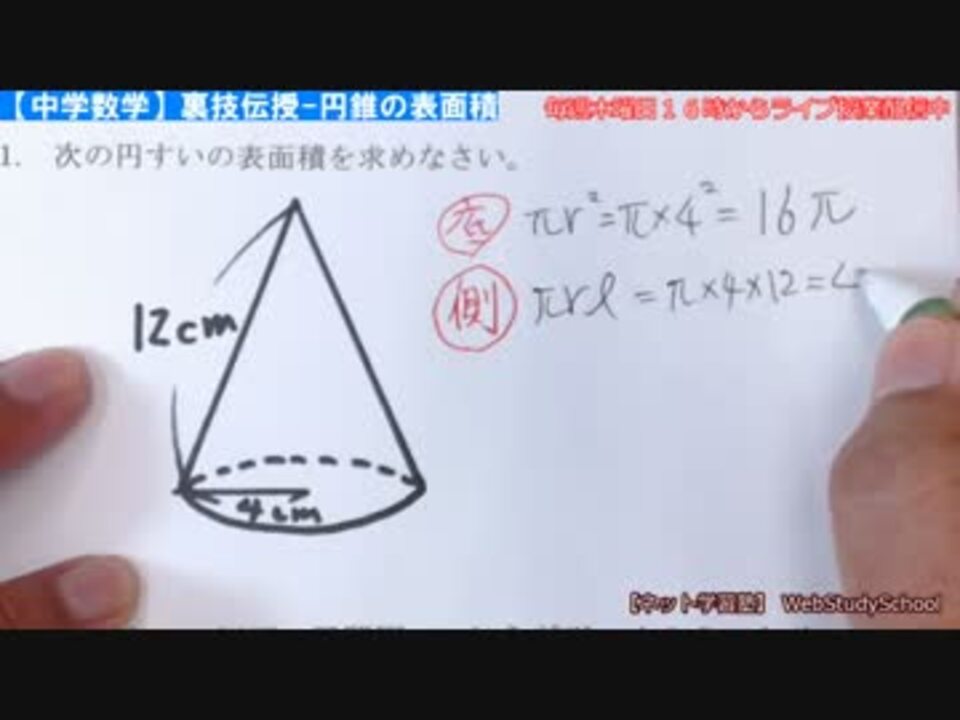



中学数学 裏技伝授 1分で解ける円錐の表面積 中心角の求め方 ニコニコ動画




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




円錐の表面積の求め方 公式と計算例



中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル
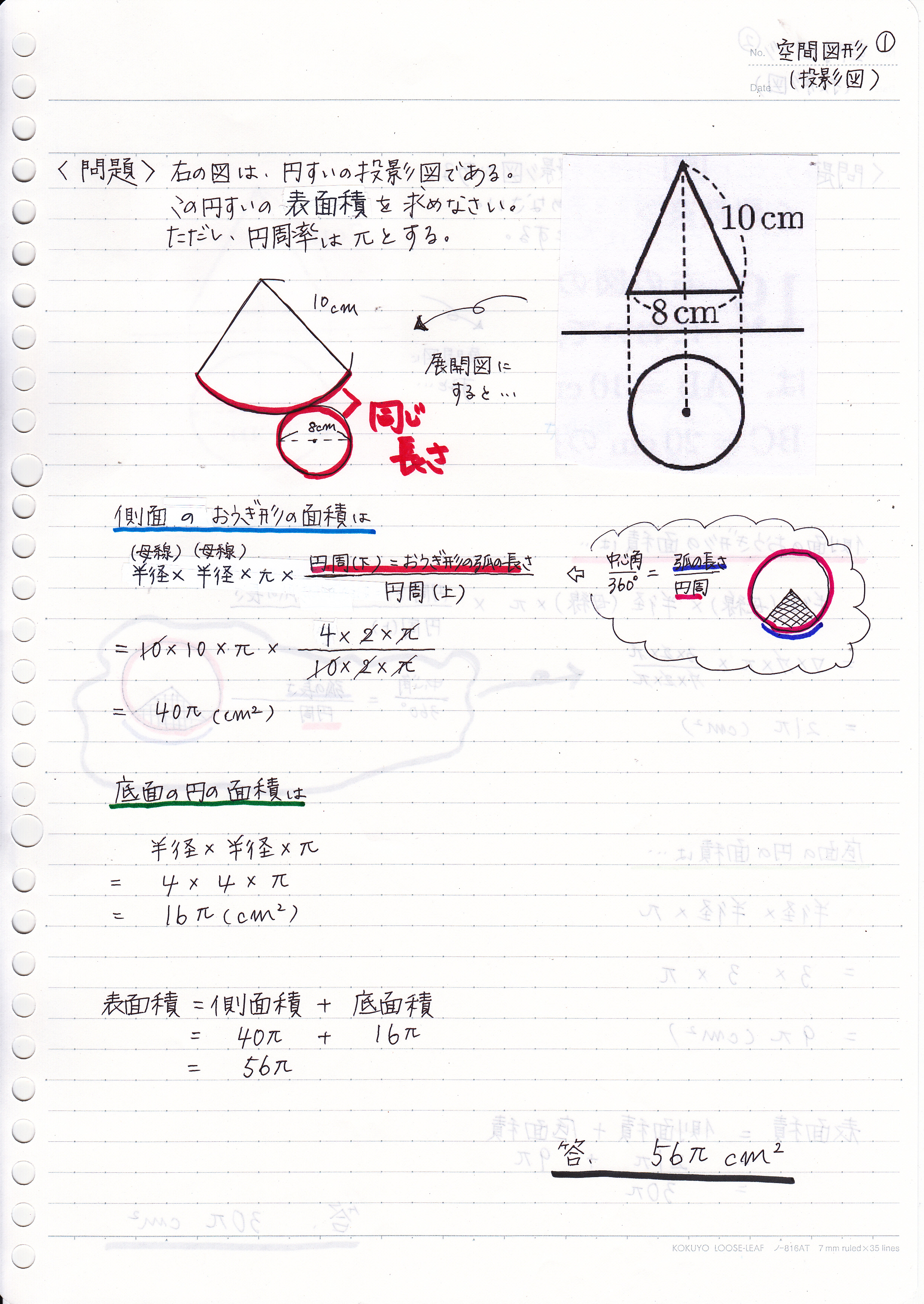



投影図から表面積を求める問題 2問 現役塾講師のわかりやすい中学数学の解き方



1




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



円すいの表面積の求め方 公式 まいにち一題 中学受験過去問題研究




円錐の表面積を 公式を使って求める チーム エン
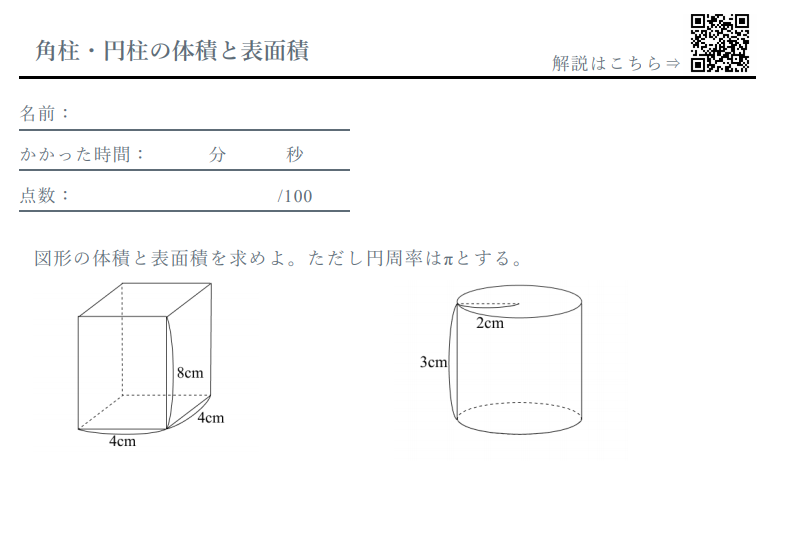



角柱 円柱の体積と表面積 計算ドリル 問題集 数学fun




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo



1



Math 横にした円錐が転がる問題 中学生 働きアリ



中学数学 円すいに関する練習問題



数学の円錐の表面積を求める問題がわからないので 教えていただきたい Yahoo 知恵袋




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト
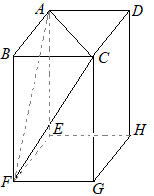



立体の表面積



円錐の表面積を超簡単に出す裏ワザ公式 個太郎塾




立体の表面積 無料で使える中学学習プリント




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
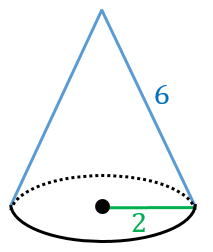



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




立体の表面積 無料で使える中学学習プリント
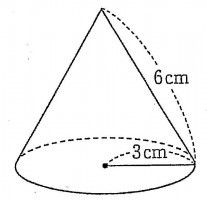



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト
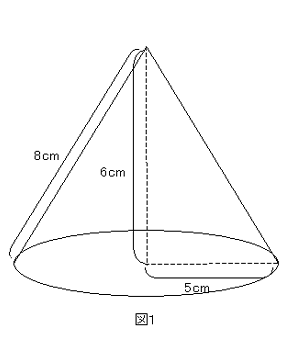



空間図形 練習問題 2 ネット塾




中間テストで出た問題です やり方がよく分かりません教えてください Clear




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方



写真の円錐の体積と表面積を求める問題なんですが この答えであっているでしょ Yahoo 知恵袋




立体の表面積 無料で使える中学学習プリント
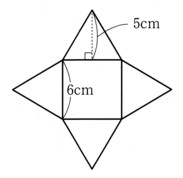



中学1年数学 立体の表面積と体積 練習問題2 解答 解説 あんのん塾




円錐の表面積の求め方 公式と計算例




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積が求めれません 円錐の表面積が求めれません 画像のよう Okwave




円錐の表面積の求め方 公式と計算例




角錐 円錐の体積と表面積の公式 数学fun




平成25年長野県立高校 入試問題 投影図から円錐の表面積を求める問題 現役塾講師のわかりやすい中学数学の解き方
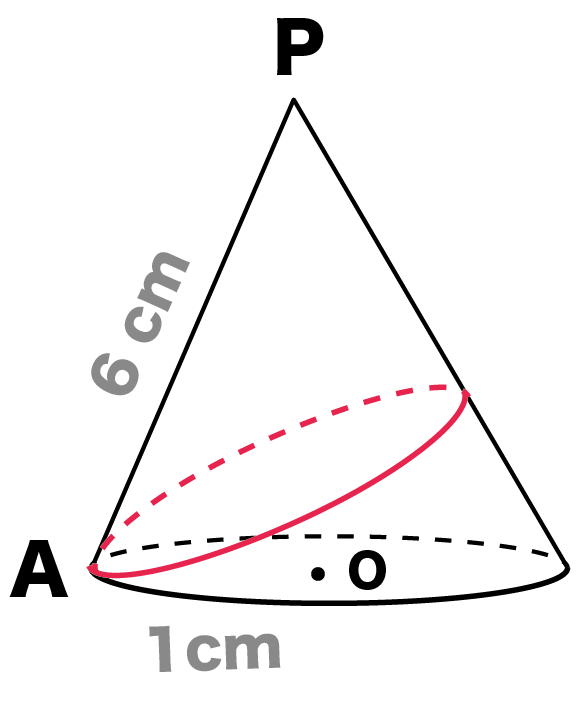



円錐にかけたひもの最短距離を求める3ステップ Qikeru 学びを楽しくわかりやすく



立体の表面積




至急です 空間図形の問題がわかりません 解説お願いします Clear




円錐の表面積の求め方 公式と計算例




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
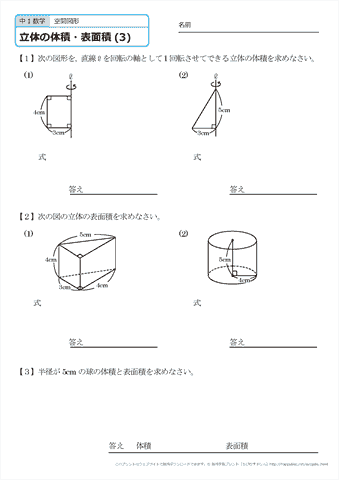



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




毎日問題を解こう 27 苦手な数学を簡単に




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




この問題の円錐の底面積の半径の求め方を教えてください Clear




中1数学 円すいの問題 練習編 映像授業のtry It トライイット
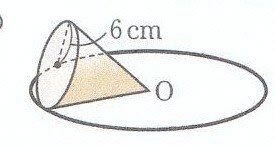



円すいの表面積を求める 数友で入試問題を解こう 2 べんきょうなせん W



Math 横にした円錐が転がる問題 中学生 働きアリ




立体の表面積 無料で使える中学学習プリント




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1
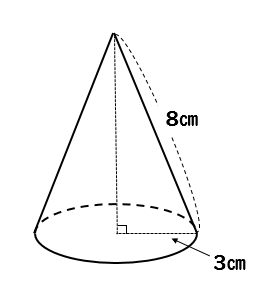



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




円錐の表面積の求め方 中学1年数学 Youtube




公式を図解 すい体の体積 円すいの表面積の求め方



0 件のコメント:
コメントを投稿