Hint Drag to pan Mouse wheel to zoom Graph of the parabola in vertex form The vertex form of parabola equation is y = a (x h)^2 k, where (h, k) = vertex and axis of symmetry x = h The parabola is f (x) = y = 2x2 4x 3 Write the equation in vertex form of a parabola eqaution Divide each side by negative 2 y/2 = x2 2x 3 /2To graph a linear equation in slopeintercept form, we can use the information given by that form For example, y=2x3 tells us that the slope of the line is 2 and the yintercept is at (0,3) This gives us one point the line goes through, and the direction
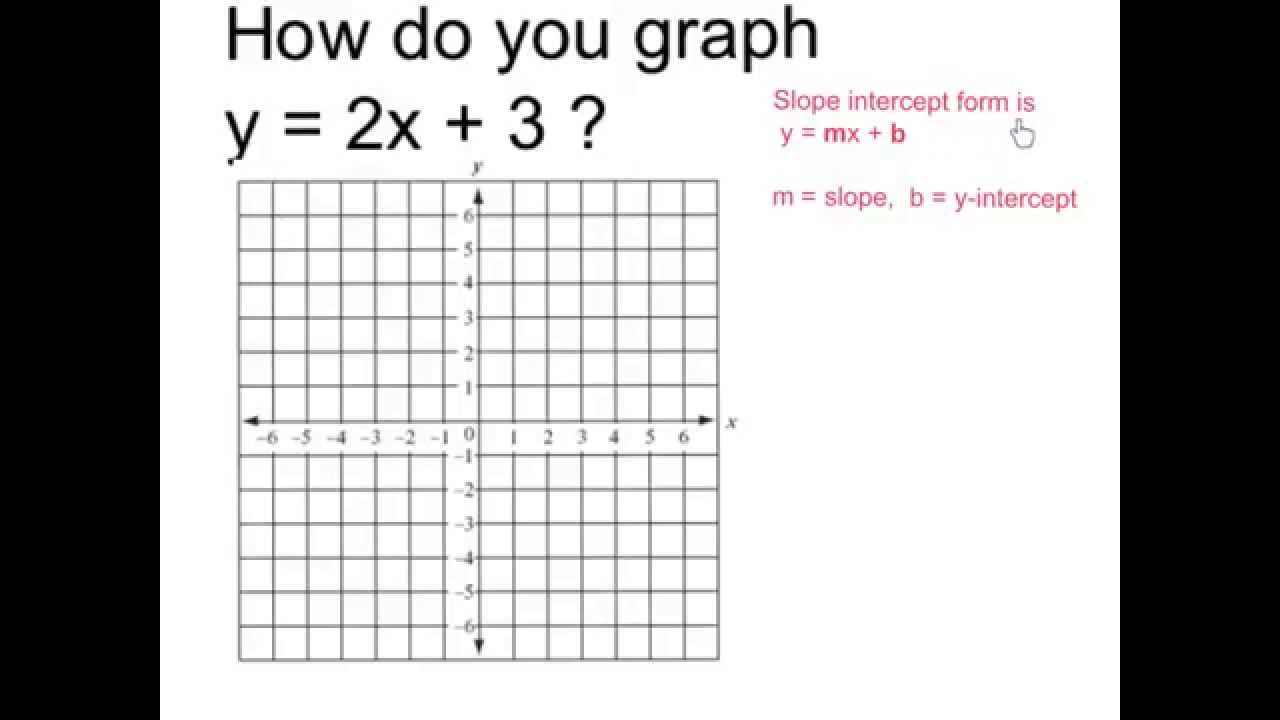
Graph Y 2x 3 Youtube
Y=x^2+2x-3 in graphing form
Y=x^2+2x-3 in graphing form-Up What is the axis of symmetry and concavity?We are given the linear function {eq}y=\frac{3}{2}x4 {/eq} We want to graph the given linear function So, we have Solution The given linear function is in the slopeintercept form {eq}y
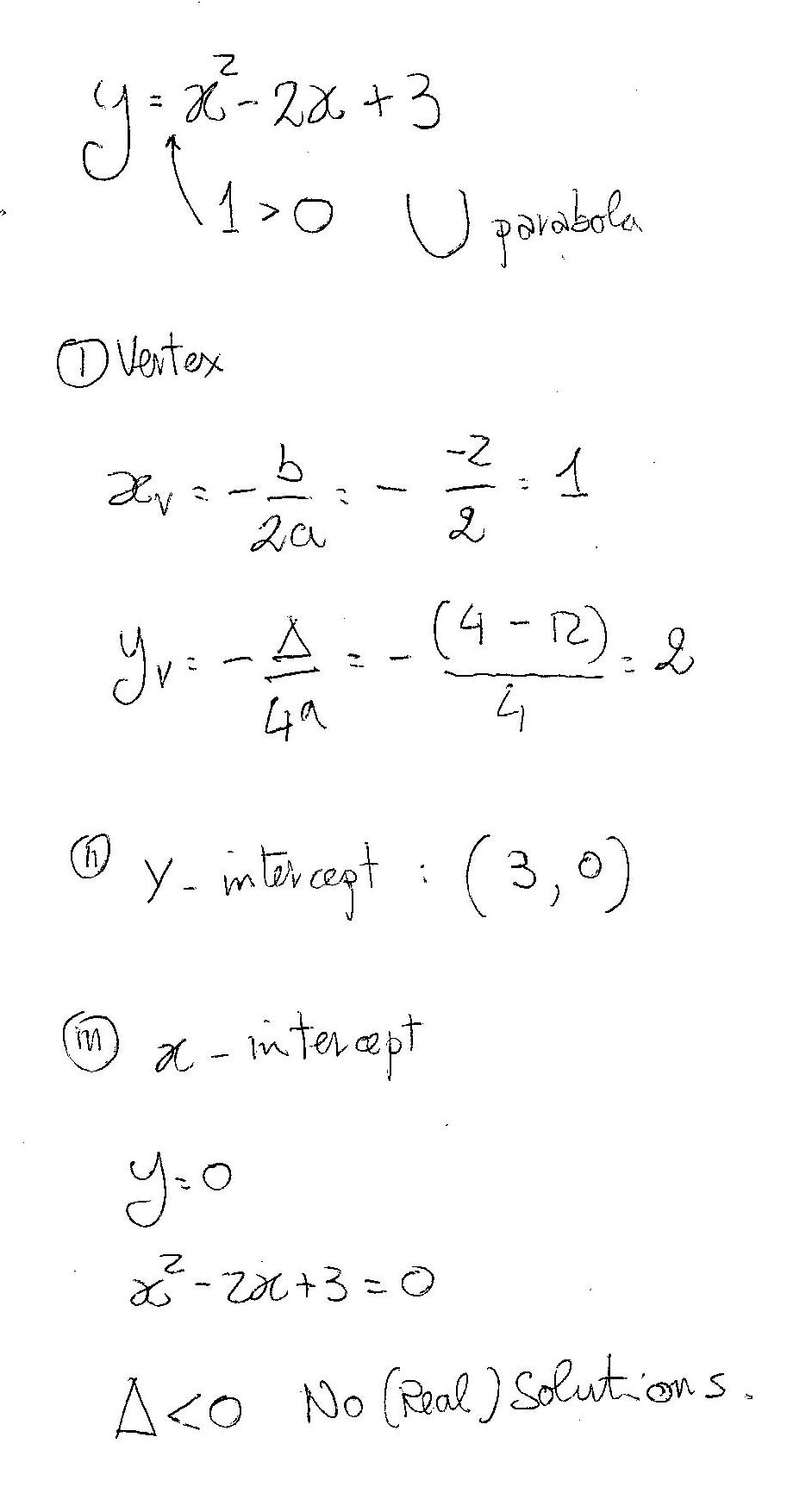



How Do You Graph Y X 2 2x 3 Socratic
The inequalities are 2x 3y ≥ 6, x y ≥ 3 and y ≤ 2 Rewrite the inequalities so that solves for y , That's the slope intercept form and it will make the boundary line easier to graph 1) Draw the coordinate plane The first inequality 2x 3y ≥ 6 3y ≥ 2x 6 y ≥ ( 2/3)x 2 2) Graph the line y = ( 2/3)x 2 3) Since the inequality symbol is ≥ the boundary is \(2 x3 y=6, \quad 3 x=4 y7, \quad y=2 x5, \quad 2 y=3, \quad \text { and } \quad x2=0\) A line is completely determined by two points Therefore, to graph a linear equation, we need to find the coordinates of two points This can be accomplished by choosing an arbitrary value for x or y and then solving for the other variableAfter you enter the expression, Algebra Calculator will graph the equation y=2x1 Here are more examples of how to graph equations in Algebra Calculator Feel free to try them now Graph y=x^22x y=x^22x Graph y= (x3)^2 y= (x3)^2
Y = x 2 2x 3 is a parabola Since the x 2 is positive, it opens upward (concaveup) If you factor the right hand side, you get (x1) (x3) so that means that the xintercepts are at 1 and 3 The vertex is halfway between these of course (at x = 1) That means the vertex is at x = 1 and y = 1 2Y = x²4x3 (0,3); In this function, x = 1 would make y = 8/0 which is undefined To find this, just set the denominator equal to zero and solve for x 2x 2 = 0 2x = 2 x = 1 The function is defined for all other numbers, so the domain is (infinity, 1)U(1, infinity) I can't remember off hand any good way to find the range other than graphing the function
Changing "c" only changes the vertical position of the graph, not it's shape The parabola y = x 2 2 is raised two units above the graph y = x 2 Similarly, the graph of y = x 2 3 is 3 units below the graph of y = x 2 The constant term "c" has the same effect for any value of a and b Parabolas in the vertexform or the ahk form, y = a(x y=(x1)^216 >"the equation of a parabola in "color(blue)"vertex form" is •color(white)(x)y=a(xh)^2k "where "(h,k)" are the coordinates of the vertex and a" "is a multiplier" "to obtain this form "color(blue)"complete the square" y=x^22(1)x color(red)(1)color(red)(1)15 y=(x1)^216larrcolor(red)"in vertex form" To graph this, we'll need y y intercepts We find these just like we found x x intercepts in the previous couple of problems y 2 − 6 y 5 = 0 ( y − 5) ( y − 1) = 0 y 2 − 6 y 5 = 0 ( y − 5) ( y − 1) = 0 The parabola will have y y intercepts at y = 1 y = 1 and y = 5 y = 5 Here's a sketch of the graph



Math Spoken Here Classes Quadratic Equations 3



What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic
Let us put a circle of radius 5 on a graph x 2 y 2 − 2x − 4y − 4 = 0 It is a circle equation, but "in disguise"!60 Chapter 2 Graphing and Writing Linear Equations 23 Lesson Lesson Tutorials Key Vocabulary xintercept, p 60 yintercept, p 60 slopeintercept form, p 60 Intercepts The xintercept of a line is the xcoordinate of the point where the line crosses the xaxisIt occurs when y = 0 The yintercept of a line is the ycoordinate of the point where the line crosses the yaxisAnd Standard Form Learn vocabulary, terms, and more with flashcards, games, and other study tools



Quadratics Graphing Parabolas Sparknotes




Vertex Intercept And Standard Form Ck 12 Foundation
Y = a(xh)^2 k is the general form of a parabola opening Up or Down, a = 1 > 0, parabola opens Up 3rd Step what is the Line of symmetry x = 1For x = 2, y = 2 2 0 for x = 3, y = 3 2 = 5 and we obtain the solutions (0,2), (3,1), (2,0), and (3,5) which can be displayed in a tabular form as shown below If we graph the points determined by these ordered pairs and pass a straight line through them, we obtain the graph of all solutions of y = x 2, as shown in Figure 73The slopeintercept form of the equation of a line is a useful form for graphing as well as for understanding the relationship between x and y In this lesson, learn how the slopeintercept form




Chapter 6 Ppt Algebra



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic
23 Graphing SlopeIntercept Form Objective Give the equation of a line with a known slope and yintercept When graphing a line we found one method we could use is to make a table of values However, if we can identify some properties of the line, we may be able to y=2x 5 2) y= − 6x 4 3) y= x − 4 4) y= − x − 2Y=3x1 Polynomials Algebra Calculator can simplify polynomials, but it only supports polynomials containing the variable x Here are some examplesWrite the quadratic equation in standard form and determine if the graph opens up or down 1) y = 2x2 x – 1 2) y = 3 – x – x2 3) y = 3x2 1 – 4x 4) y = 4 – 3x 2 5) y = x 9x2 6) y = 3x 5x2–3x2 Vertex the lowest or the highest point of the graph Axis of Symmetry the vertical line through the vertex



Draw The Graph Of Y 2x 2 X 6 Mathskey Com



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf
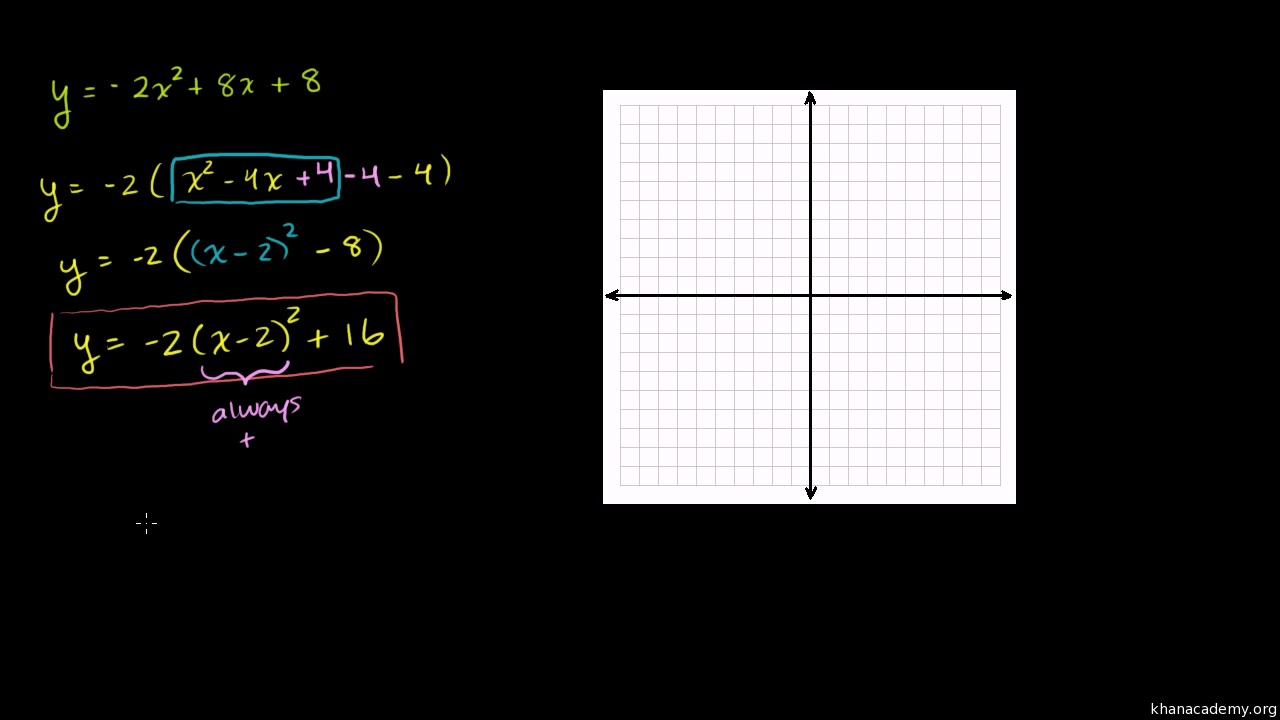
Rewrite in \(y=a(x−h)^{2}k\) form and determine the vertex \(y=2x^{2}−4x8\) Solution Since a = 2, factor this out of the first two terms in order to complete the square Leave room inside the parentheses to add a constant term Now use −2 to determine the value that completes the square In this case, \(\frac{(2)^{2}}{2}=\((1)^{2}=1\)Graph y=2x^2x3 y = 2x2 x − 3 y = 2 x 2 x 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for 2 x 2 x − 3 2 x 2 x 3Slopeintercept form Slope yintercept graph 1) Y = 5x 6 2) Y = ¾ x 1 3) Y = 1/4 x 3 4) Y = 2x 5 5) Y = 3/2 x 1 6) Y = 6x 1 Finding equations from graphs For each graph, find the slope, yintercept, the equation of the line that would be drawn through the points on each graph and three points on the line 1




Solve The Equation X 2 2x 3 0 Graphically




Shifting Parabolas Video Khan Academy
Draw the graph of y=(2x–3)(x–1) for the interval –2 ≤ x ≤ 4 ;A shift to the right means moving in the positive \(x\) direction, therefore \(x\) is replaced with \(x 2\) and the new equation is \(y = 3(x 2)^2 1\) Eric's answer We replace \(x\) with \(x – 2\), therefore the new equation is \(y = 3(x – 2)^2 1\) Work together in pairs Discuss the two different answers and decide which one is correctMethod 3 Using the x and yintercepts When graphing linear equations that are given in the form y = m x b, it is easiest to just apply method 2 But sometimes, linear equations are given in standard form A x B y = C, where A, B, and C are positive or negative whole numbers In this case, using the x and yintercept may be the quickest




Graph Y 2x 3 Youtube
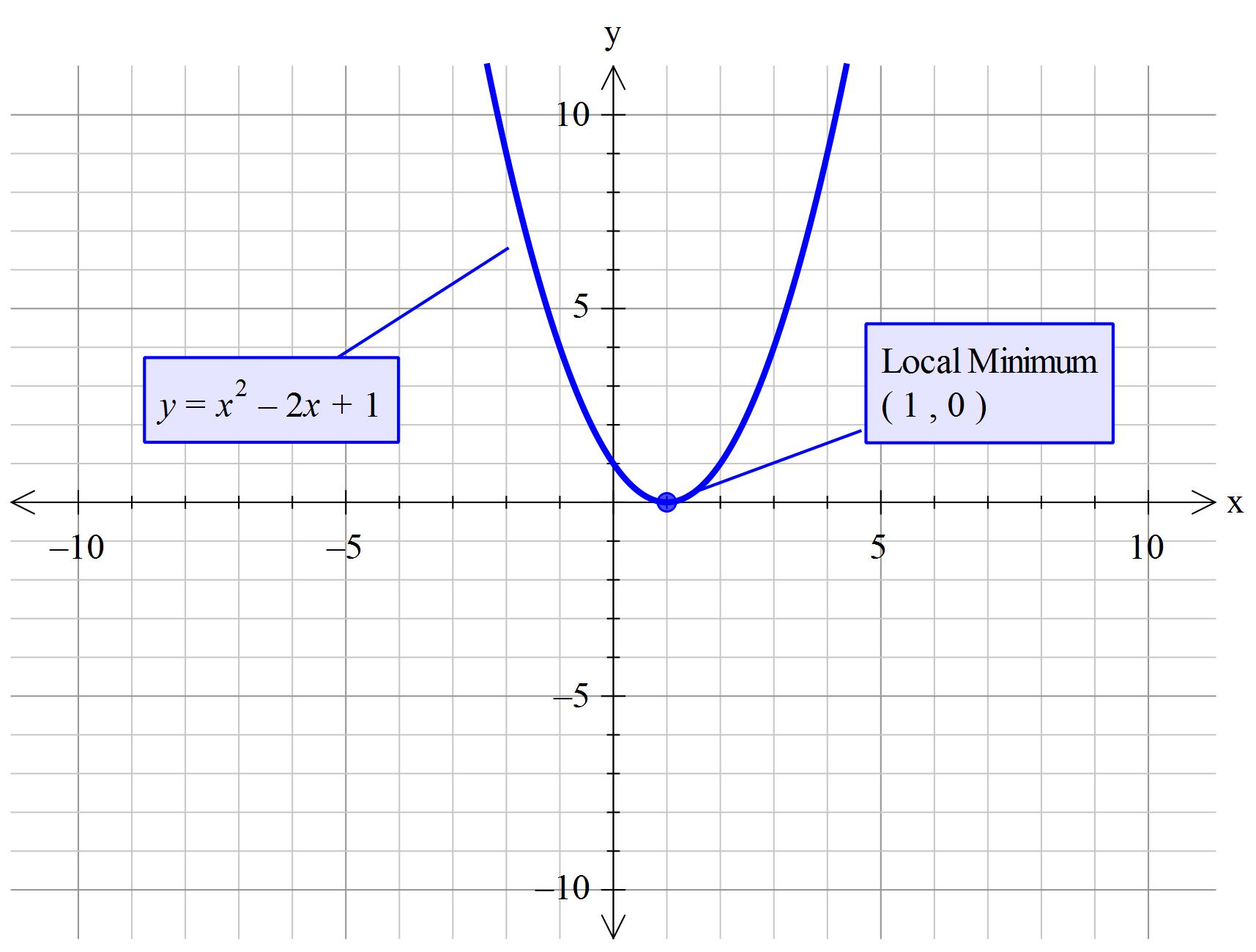



What Is The Vertex Of Y X 2 2x 1 Socratic
Graph the two lines 2x 3y = 18 3x 4y > 16 Give the Domain and Range, Slope, and Yintercept for each line Graph each equation above on the graph below and show all work Give the Domain and Range, Slope, and Yintercept for algebra PLEASE HELP!!Subtract y from both sides x^ {2}2x3y=0 − x 2 − 2 x 3 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 3y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0 #y=x^22x3# is a quadratic equation in standard form, #axbxc#, where #a=1, b=2, c=3# The graph of a quadratic equation is a parabola You need the axis of symmetry, the vertex, and the xintercepts Axis of Symmetry The axis of symmetry is an imaginary line dividing the parabola into two equal halves




5 Write The Equation Of The Parabola In Vertex Form Chegg Com




Graphing Parabolas
Important 1st Step For graphing 2nd step Which direction does the Parabola Open?As stated previously, the graph of y=x 2 is our standard graph Also, y = x 2 h shifts the graph only up or down, depending upon whether the value of h is positive or negative, respectively Thus, the graph of y = x 2 2 (red) and y = x 2 3 are illustrated below in Figure 5 Note the left and right shifts, respectivelyChapter 5 Functions Learners must be able to determine the equation of a function from a given graph Discuss and explain the characteristics of functions domain, range, intercepts with the axes, maximum and minimum values, symmetry, etc




How To Graph Y 1 2x 3 Youtube




3 2 Quadratic Functions Mathematics Libretexts
Y=x^22x4 Note (0,4)is where Parabola crosses the y axis y = (x1)^2 1 4 V(1,3) Yes!Y = x2 − 2x − 3 y = x 2 2 x 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 3 x 2 2 x 3 Tap for more steps Use the form a x 2 b x c a x 2 b xLet's say if you put x=2 in y=2x3 ,you get 'y' as 7 But when you put x=2 in y =2x3 ,you get y as 7 ,therefore 'y' can be 7 or 7 as absolute of any value is always positive ie 7=7=7 So , whatever value of 'x' you will put in y =2x3 ,you will get two values of 'y' where one value is negative of another




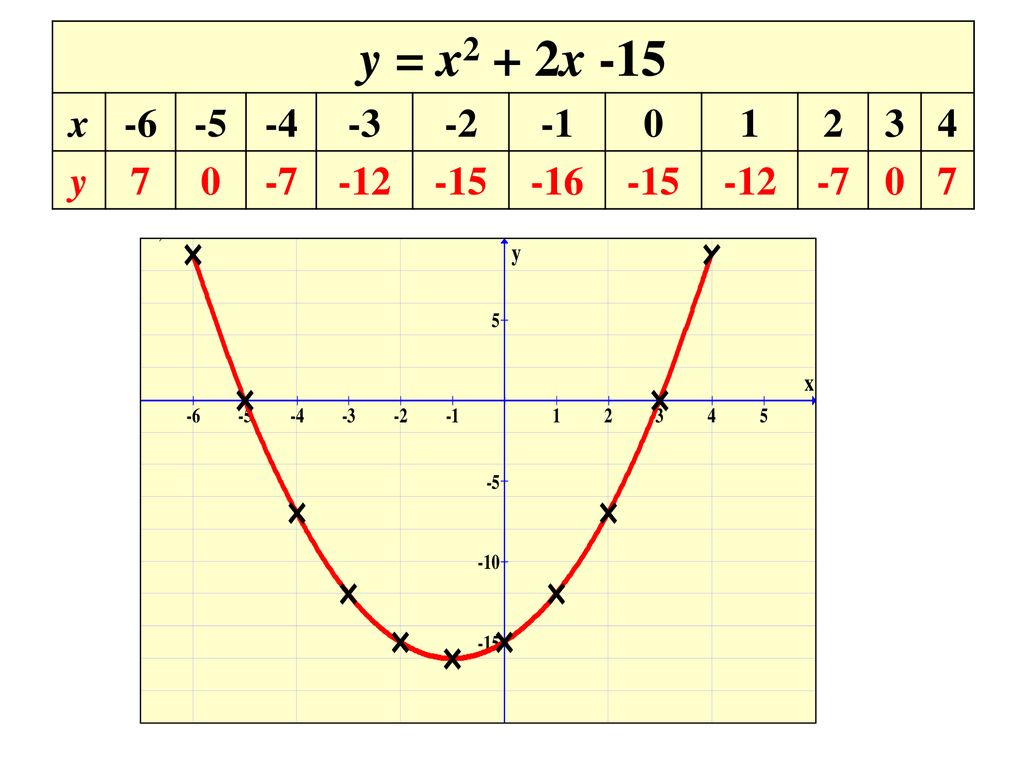
Answered Given The Relation Y X 2x 3 15 Bartleby
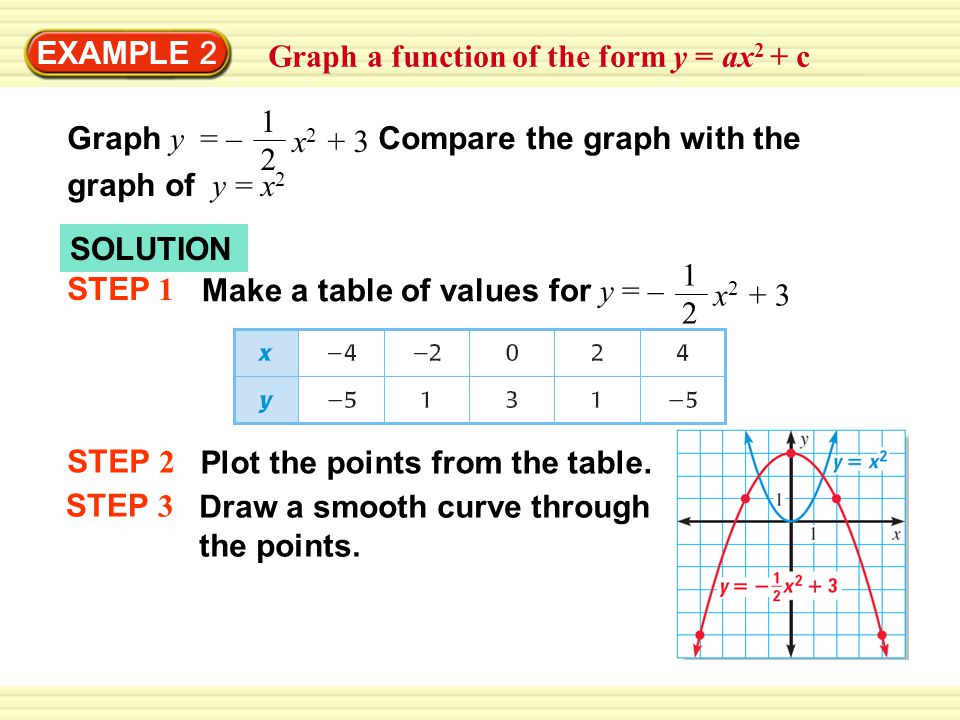



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download
Free System of Inequalities calculator Graph system of inequalities and find intersections stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyY = x²2x3 x=1 What is the yintercept and concavity?Note General Form always has x 2 y 2 for the first two terms Going From General Form to Standard Form Now imagine we have an equation in General Form x 2 y 2



Quadratics Graphing Parabolas Sparknotes




13 Convert Y X2 4x 1 Into Vertex Form Also Chegg Com
Use your graph to solve 2x 2 –5x3=0 ;Graphing Quadratic Functions Standard Form and Factored Form STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by MrsSmith433 Terms in this set (30) What is the axis of symmetry?X^2 2x 1 = y 4 (x1)^2 = y 4Vertex (1,4)y = x^22x–3 xintercepts Let y = 0 and solve for "x" x^2 2x 3 = 0 (x3)(x1) = 0 x = 3 or x = 1yintercept Let x = 0 and solve for "y" y = 0^2 2*03 y = 3



Search Q Y 3dx2 2x 3 Table Tbm Isch




Quadratic Functions
Start studying Lesson 31 Graphing Linear Functions Is it Linear?To graph a point, enter an ordered pair with the xcoordinate and ycoordinate separated by a comma, eg, To graph two objects, simply place a semicolon between the two commands, eg, y=2x^21;Graph y = x^22x–3 and give the vertex and x and y interceptsPut the equation in vertex formx^2 2x ?



Solution The Circle X 2 Y 2 2x 3 0 Is Stretched Horizontally By A Factor Of 2 About X 0 To Obtain An Ellipse What Is The Equation Of This Ellipse In General Form
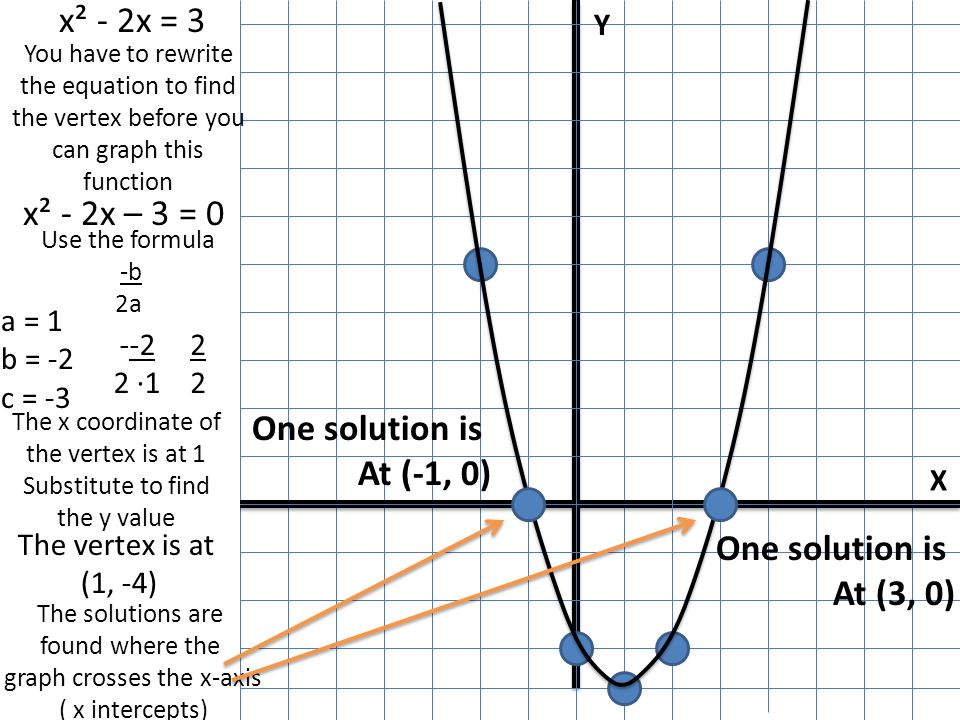



Solving Quadratic Equations By Graphing X Y I X 2x 3 You Have To Rewrite The Equation To Find The Vertex Before You Can Graph This Function Use Ppt Download
Y = 3x2 –18x 7 When a quadratic function is in standard form The equation of the line of symmetry is y = ax2 bx c, 2 b a x For example Using the formula This is best read as the opposite of b divided by the quantity of 2 times a 18 23 x 18 6 3 Thus, the line of symmetry is x = 3 D Finding the Axis of SymmetryOriginal equation 3x 2y 6 = 0 Subtract 2y from both sides to get 3x 6 = 2y Divide each side by (2) (3x 6)/(2) = (2y)/(2) → (3x)/(2) (6)/(2 The graph of y=x^22x1 is translated by the vector (2 3)The graph so obtained is reflected in the xaxis and finally it is stretched by a factor 2 parallel to yaxisFind the equation of the final graph is the form y=ax^2bxc, where a,b and c are constants to be found



Search Q Axis Of Symmetry Tbm Isch



Quadratics Graphing Parabolas Sparknotes
Right over here I have the graph of f of X and what I want to think about in this video is whether we could have sketched this graph just by looking at the definition of our function which is defined as a rational as a rational expression we have 2x plus 10 over 5x minus 15 so there's a couple of ways to do this first you might just want to pick out any numbers that are really easy to6 4 2 2 4 642 2 4 6 8 10 31B Graphing Quadratic Equations in Standard Form Acc Algebra I/Geometry A Directions Use a table to graph quadratic functionY = − 2 x − 3 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2x3=y − 2 x − 3 = y Add 3 to both sides Add 3 to both sides 2x=y3 − 2 x = y 3
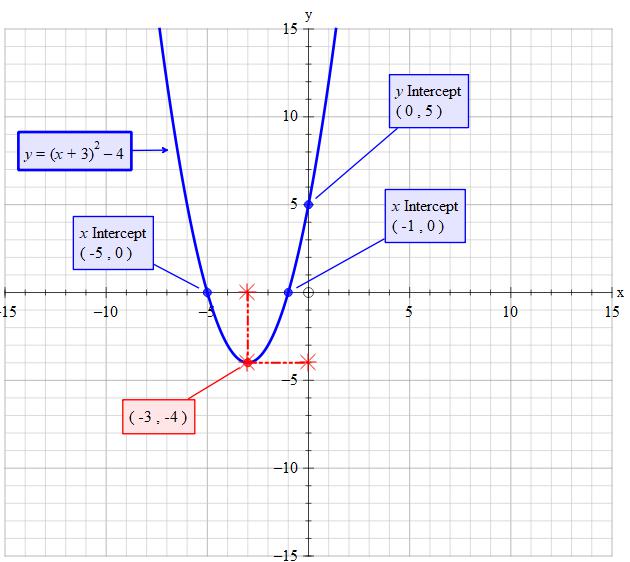



How Do You Find The Vertex And Intercepts For Y X 3 2 4 Socratic




Graphing Parabolas
All quadratic equations of the form y = a x 2 b x c have parabolic graphs with yintercept (0, c) However, not all parabolas have x intercepts Example 3 Graph y = 2 x 2 4 x 5 Solution Because the leading coefficient 2 is positive, note that the parabola opens upward Here c = 5 and the yintercept is (0, 5) To find the x
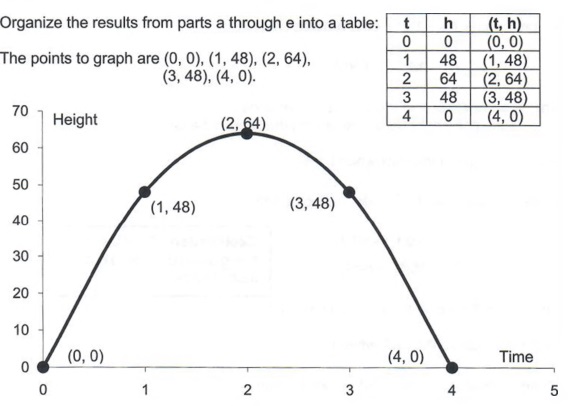



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




Draw The Graph Of Y X 2 2x 3 And Hence Find The Roots Of X 2 X 6 0
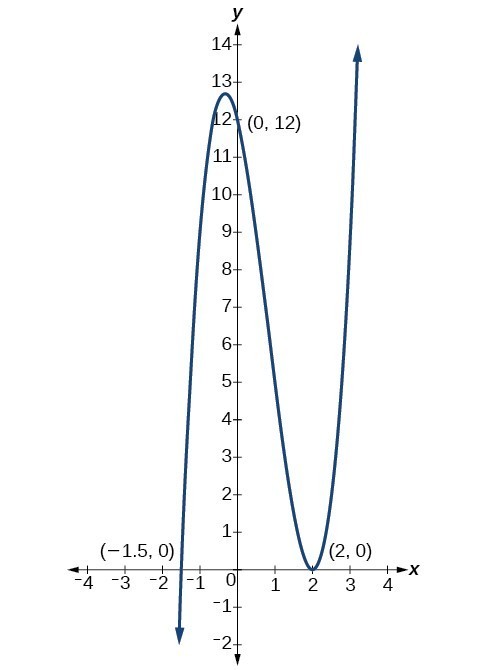



Use Factoring To find Zeros Of Polynomial Functions College Algebra



Graphing Quadratic Functions
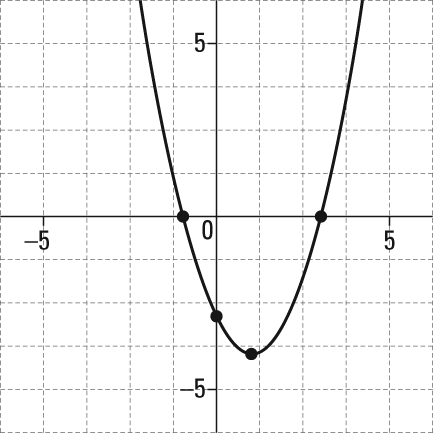



Sat Practice Questions Graphing Quadratic Functions Dummies
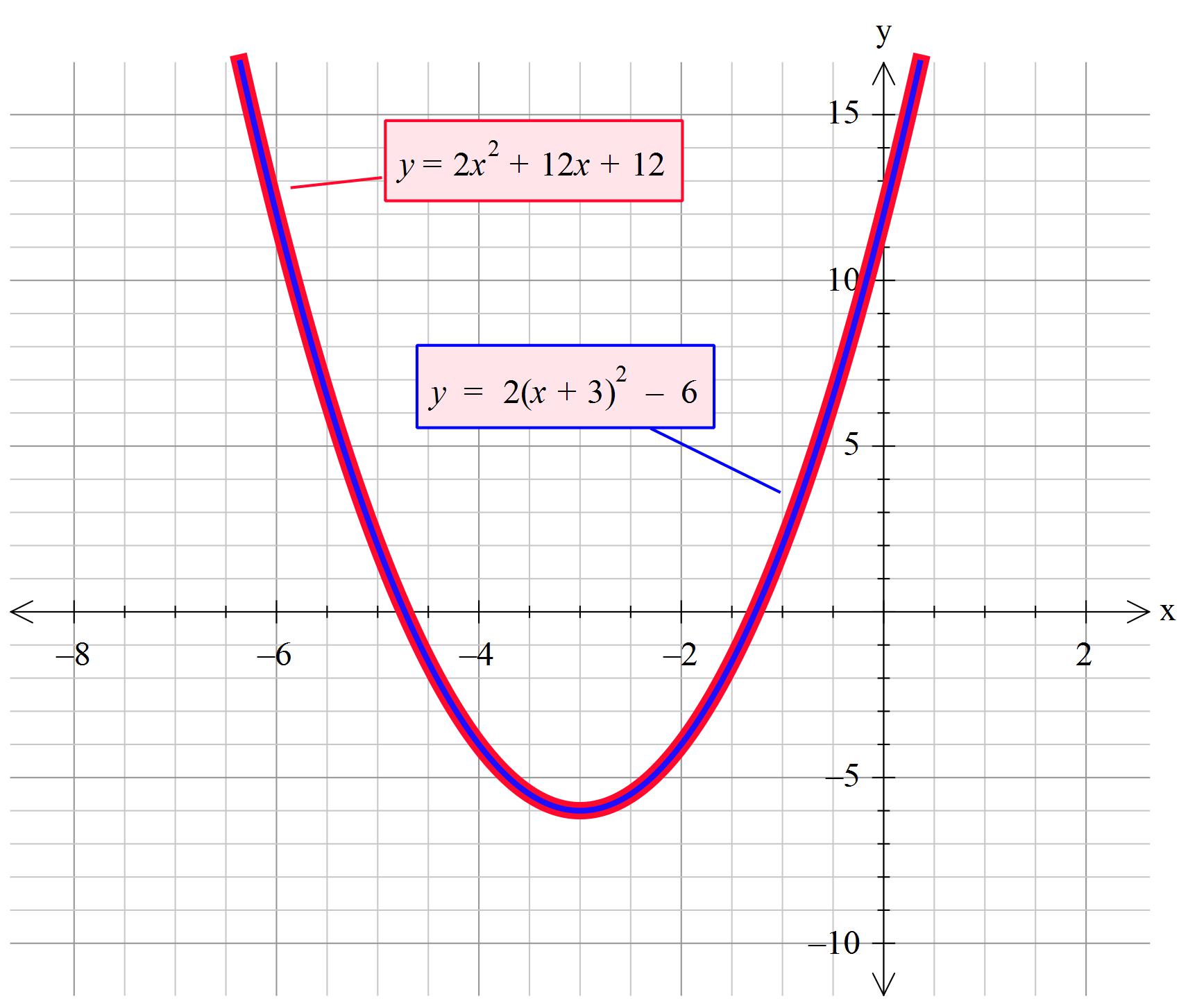



How Do You Write F X 2x 2 12x 12 In Vertex Form Socratic
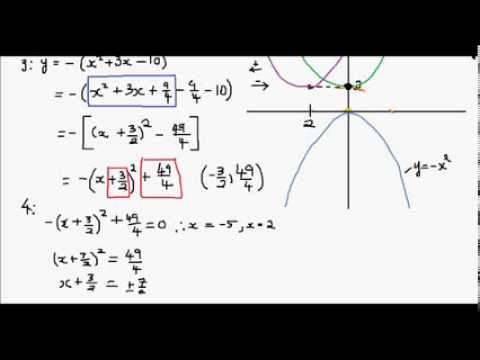



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube



1




Transformations Of Quadratic Functions College Algebra



Solution Graph Y X 2 2x 3 And Give The Vertex And X And Y Intercepts



How To Draw The Graph Of X 2 Y 2 2x 0 Quora




Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube




Using The Graphing Calculator To Graph Quadratic Equations Ck 12 Foundation




Graph Y X 2 3 Youtube




How Do You Graph Y X 2 2x Socratic



1



Quadratics




How To Graph A Quadratic Equation 10 Steps With Pictures




Example 1 Solve A Quadratic Equation Having Two Solutions Solve X 2 2x 3 By Graphing Step 1 Write The Equation In Standard Form Write Original Equation Ppt Download



Solution Y X2 2x 3 And How Do You Graph It



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf
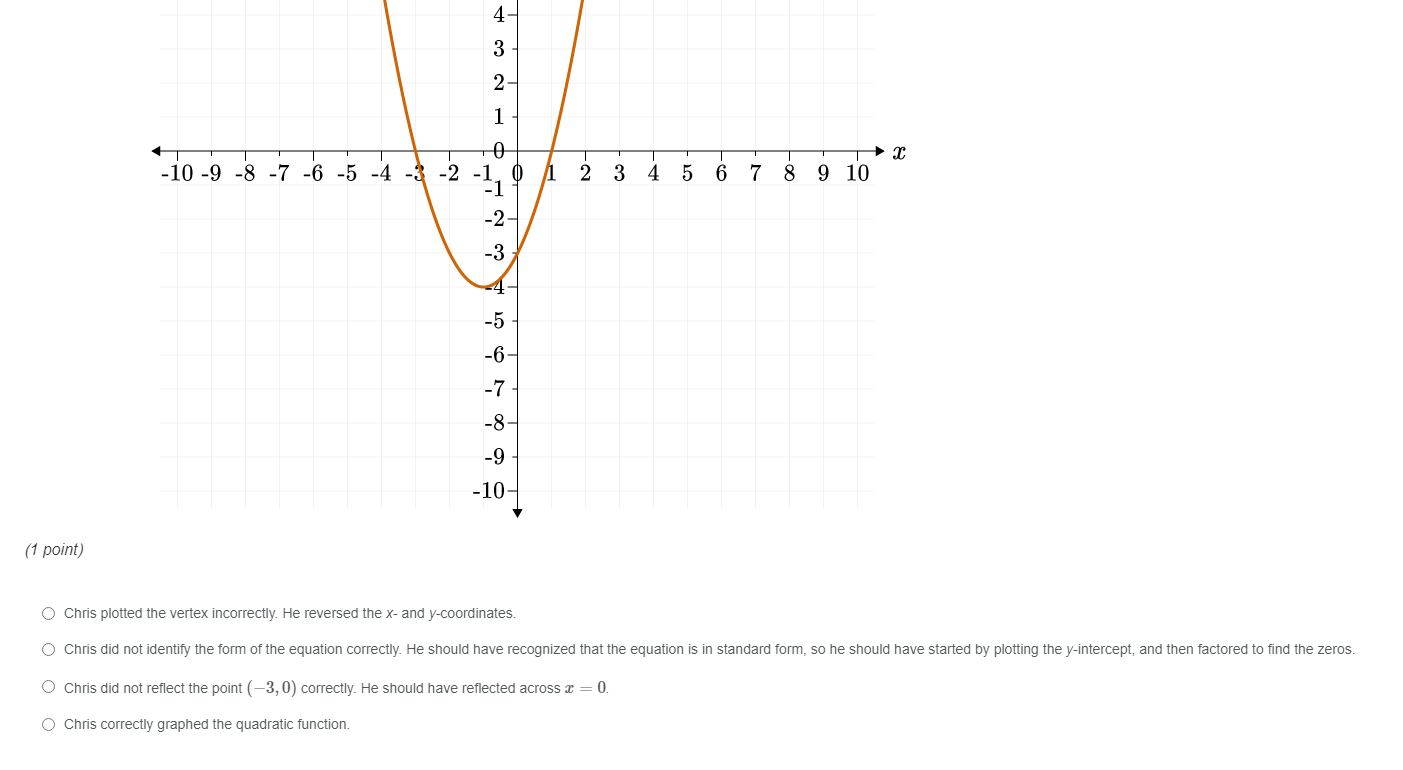



Chris Is Asked To Graph The Quadratic Function F X Chegg Com
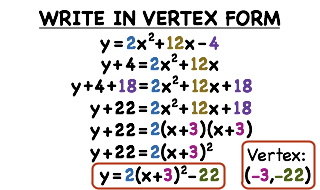



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square If A 1 Printable Summary Virtual Nerd



Graphing Quadratic Functions



Quadratic Functions
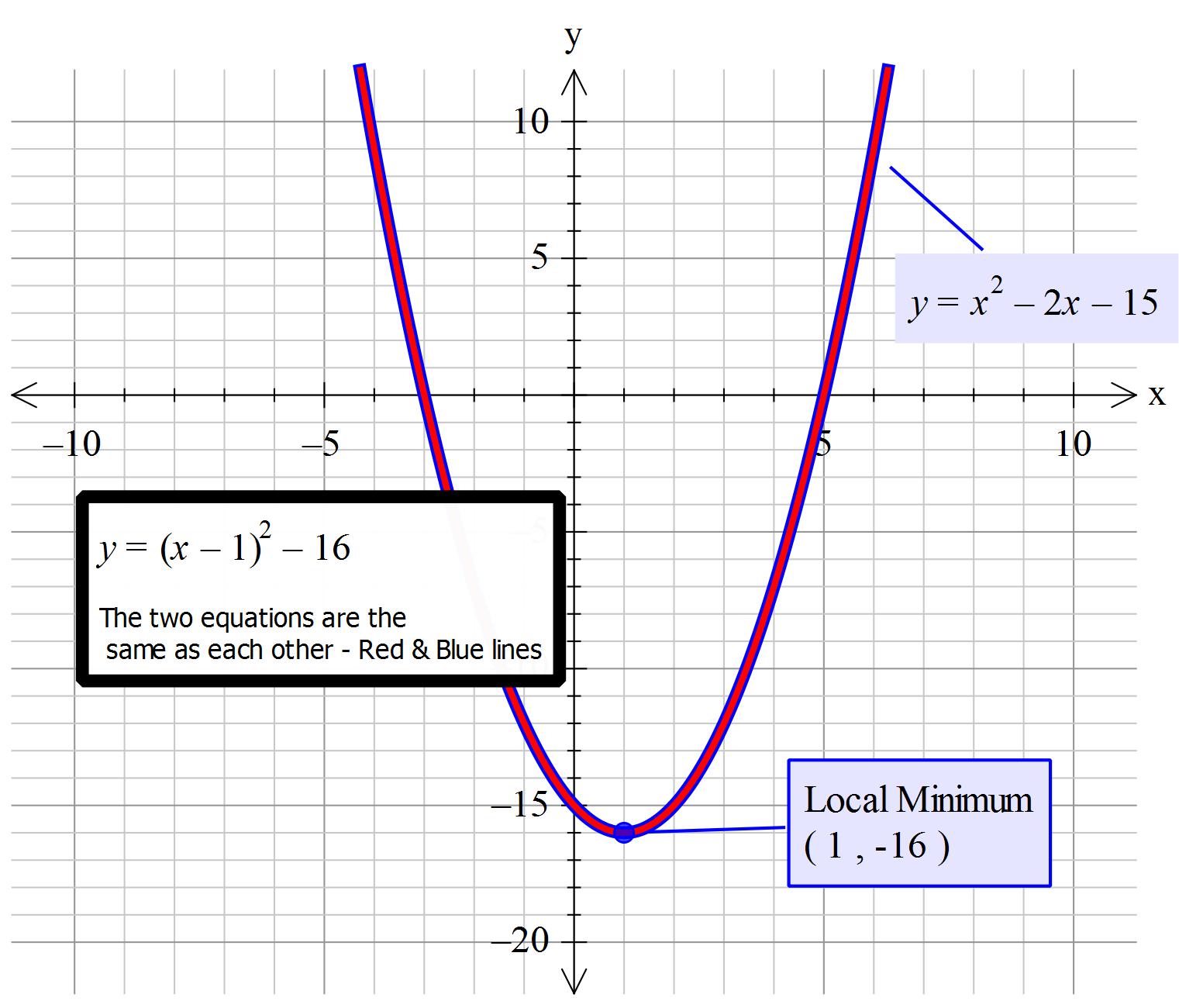



What Is The Vertex Form Of Y X 2 2x 15 Socratic
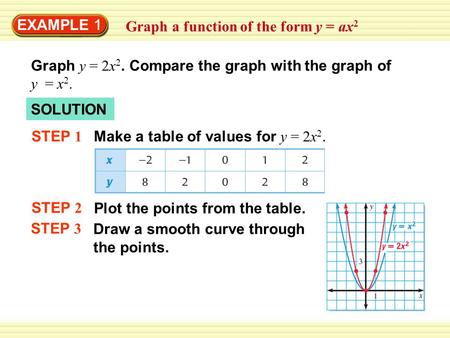



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download




1 Solve For X And Simplify The Answer B 2x2 4x 5 0 Chegg Com



Quadratics Graphing Parabolas Sparknotes
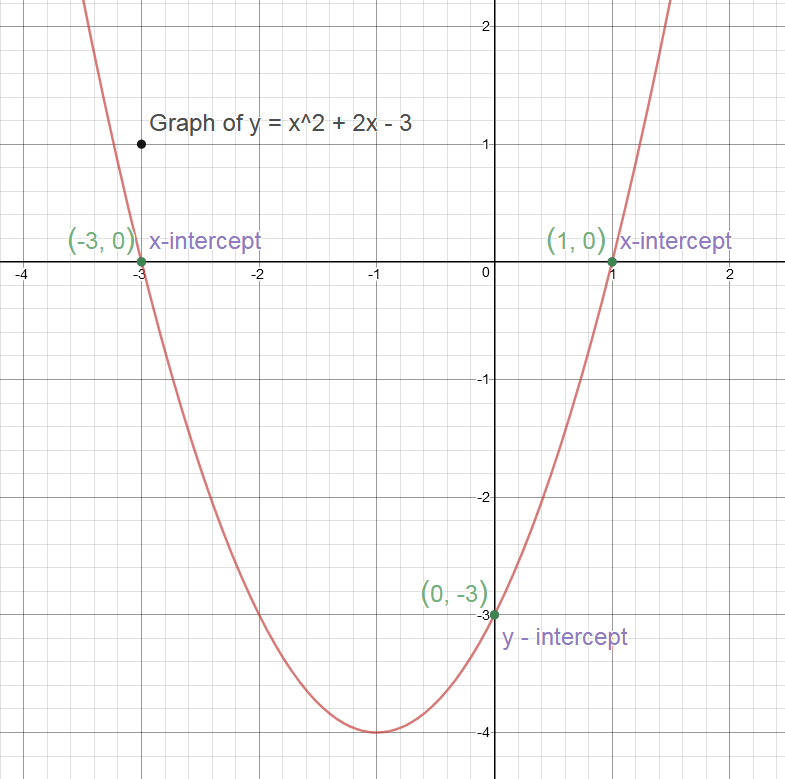



How Do You Find The X And Y Intercepts For Y X 2 2x 3 Socratic



Content Transformations Of The Parabola




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube
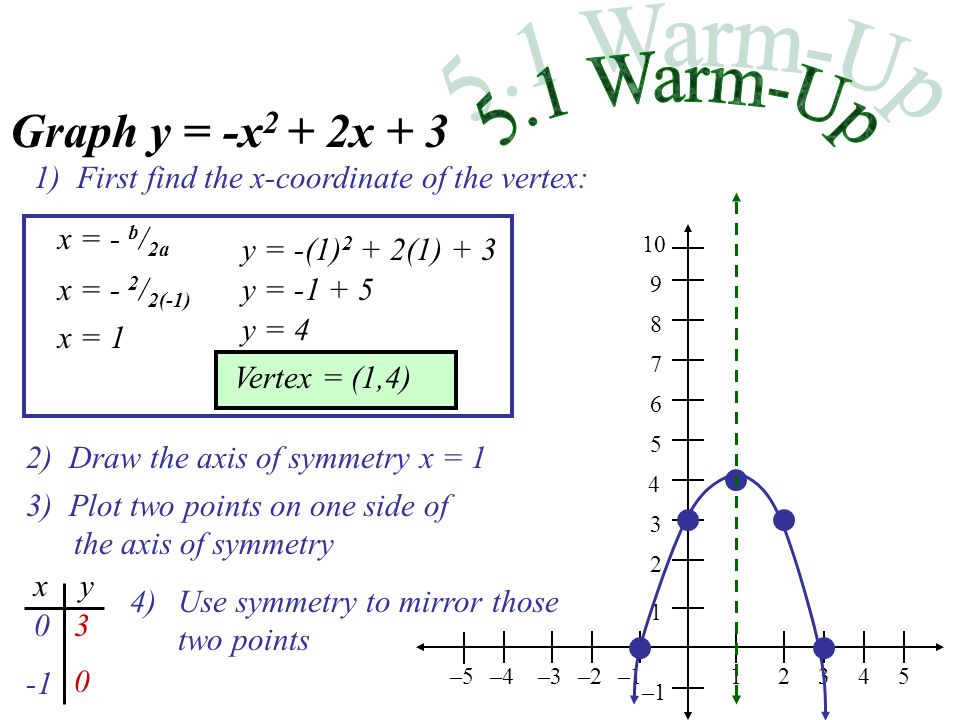



Ch 5 Notes Ppt Video Online Download




Graphing Quadratic Functions
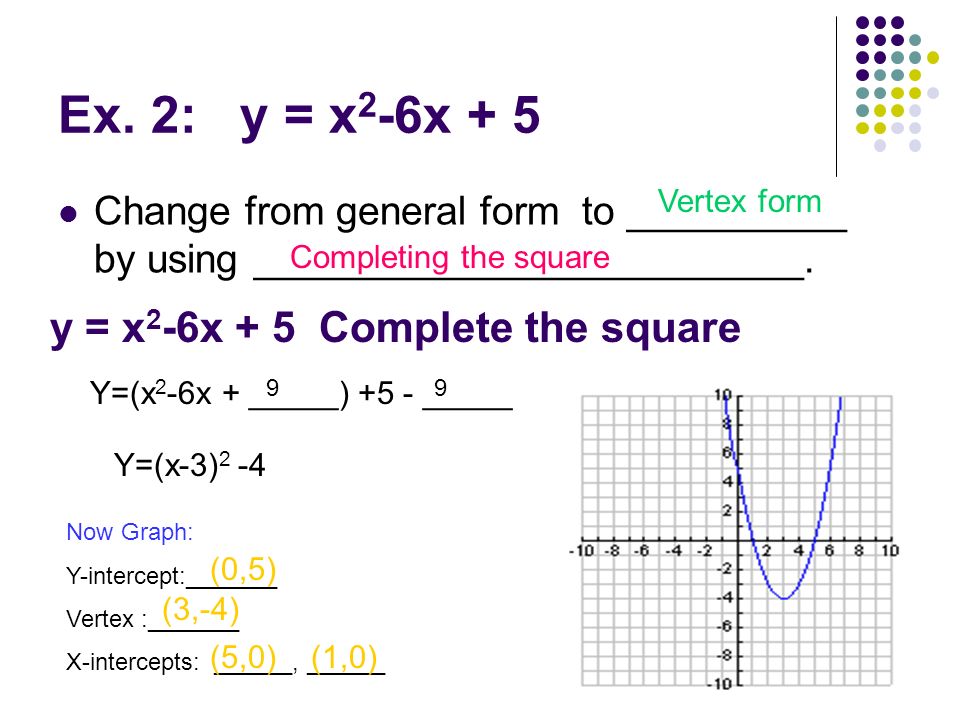



Warm Up Find The Vertex The Roots Or The Y Intercept Of The Following Forms 1 F X X 4 F X 2 X 3 X 4 3 F X X 2 2x 15 Answers Ppt Download
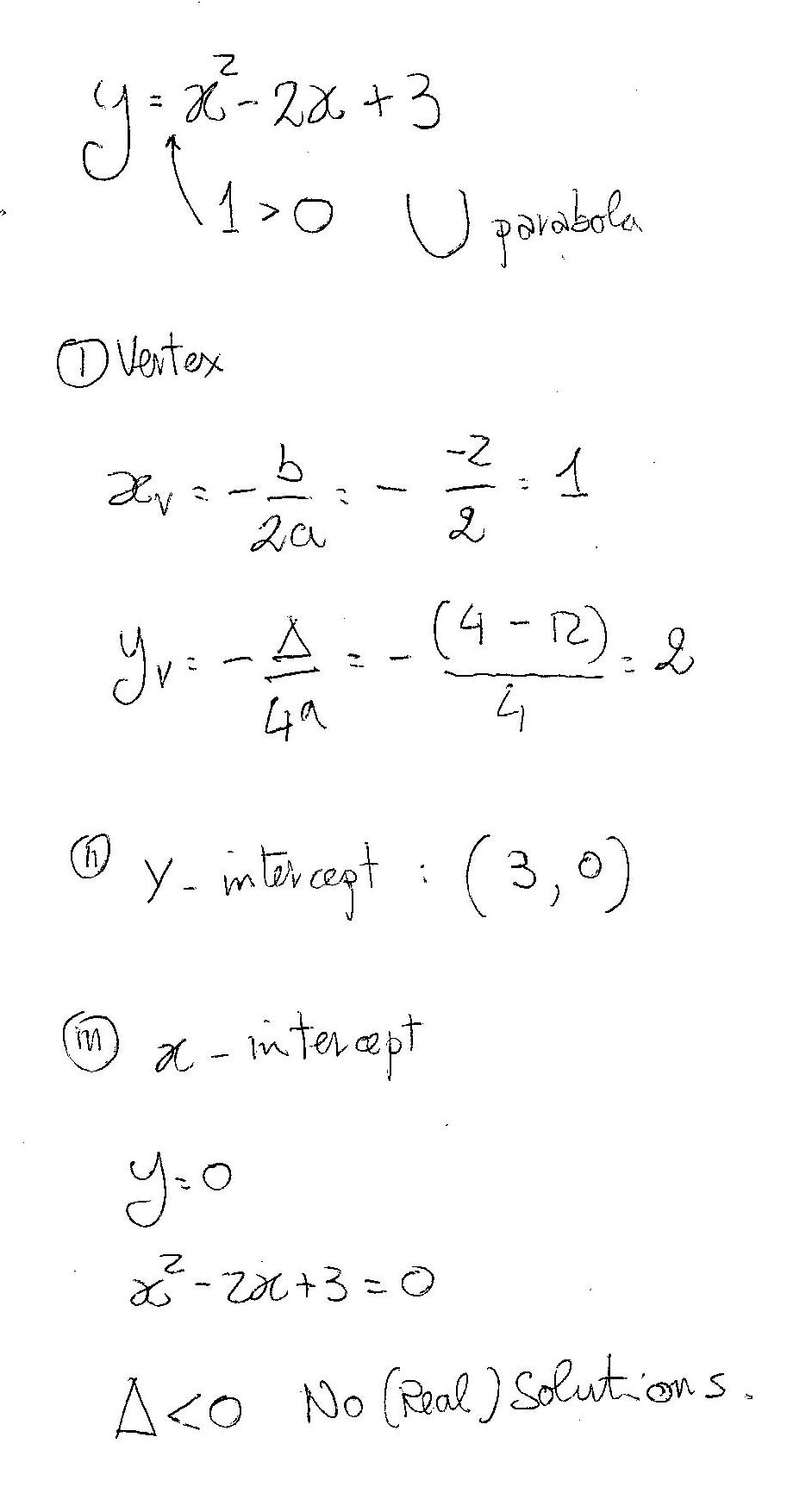



How Do You Graph Y X 2 2x 3 Socratic



Quadratics




What Is The Vertex Form Of Y X 2 5x 14 Socratic



Solve And Graph Quadratic Function 2x 2 12x 11 Mathskey Com



Graphing Quadratic Functions
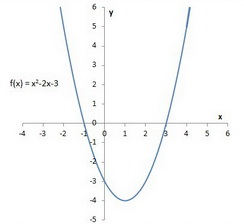



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic
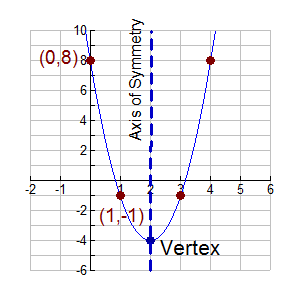



Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Http Www Mychandlerschools Org Cms Lib6 Az Centricity Domain 15 Alg q3 review Pdf



Quadratic Functions



Graphing Quadratic Functions




Name Warm Up 4 3 Use The Related Graph Of Y X 2 2x




3 Let Y F X X2 2x 3 G Express F X In Chegg Com




Graph Y X 2 2x 3 Include All Key Points Chegg Com




Quadratic Graph Example Y Ax Expii



Math Spoken Here Classes Quadratic Equations 3



How To Write An Equation For A Parabola In Vertex Form Wyzant Ask An Expert
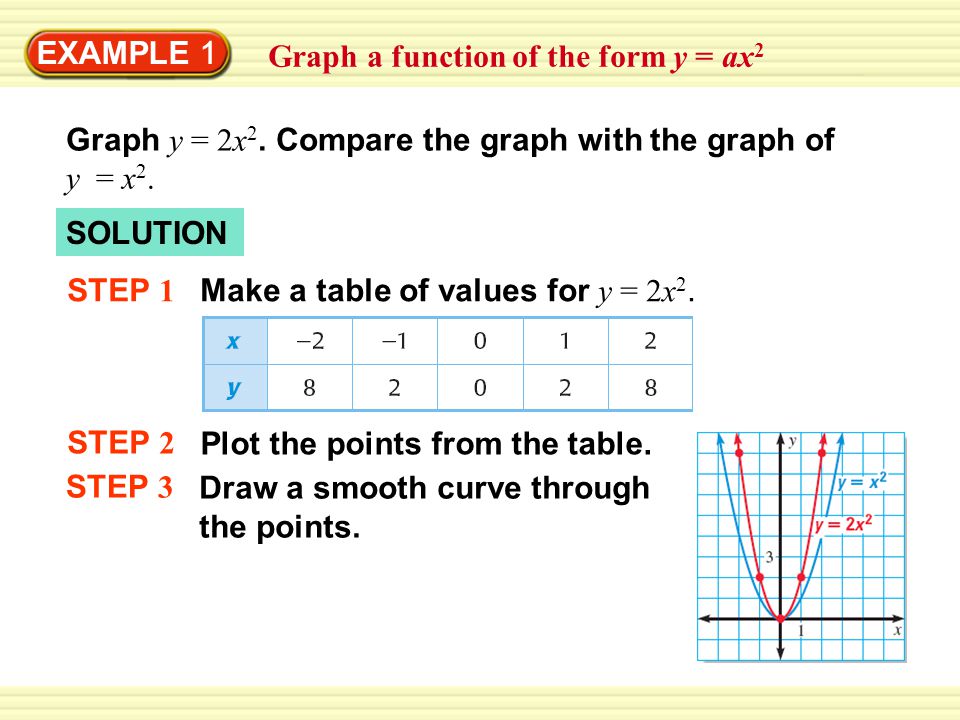



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download




Example 5 Find The Zeros Of Quadratic Functions Find The Zeros Of The Function By Rewriting The Function In Intercept Form A Y X 2 X 12 B Y Ppt Download
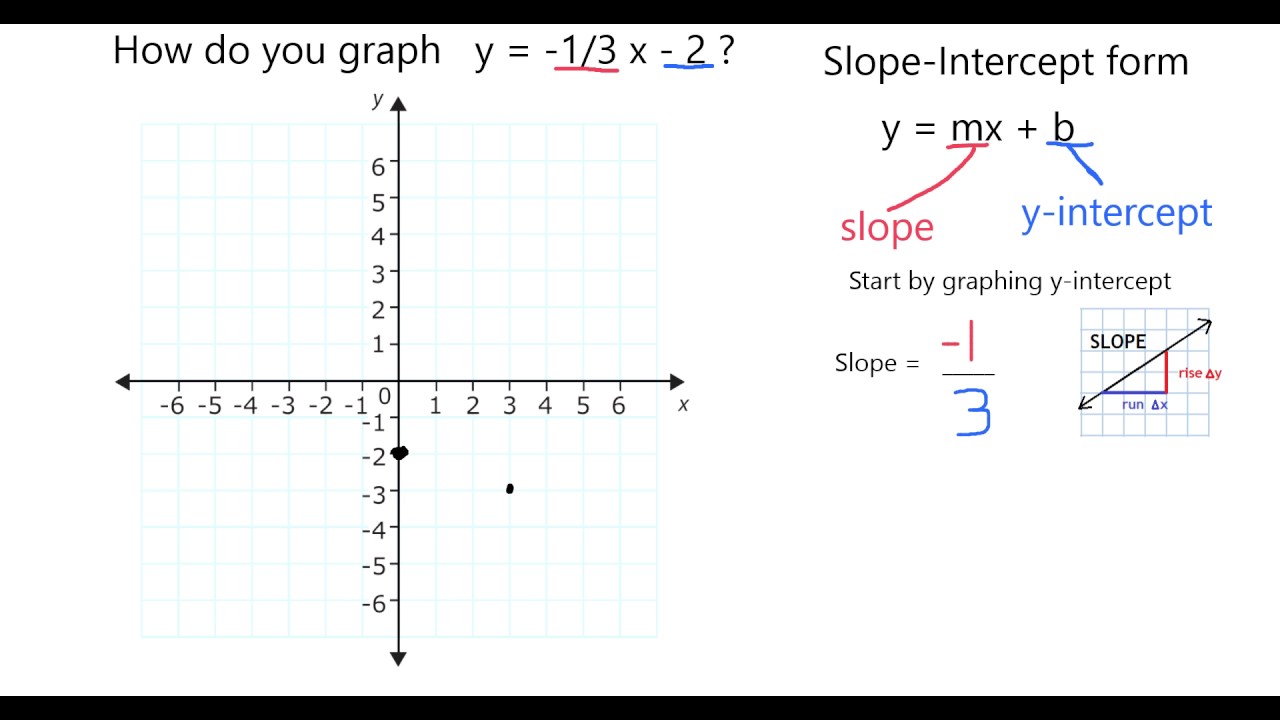



Graph In Slope Intercept Form Y 1 3 X 2 Youtube



How Do You Graph Y X 2 2x 3 Socratic




Graph Each Function Compare The Graph With The Graph Of Y X 2 Then Label The Vertex And Axis Of Symmetry 1 Y 5x 2 2 Y 4x Y 2x 2 6x Ppt Download




Graphing Parabolas



Solution What Is The Vertex Form Of F X X 2 2x 5




How To Draw Y 2 X 2 Interactive Mathematics



Systems Of Linear Equations




Section 2 Quadratic Functions
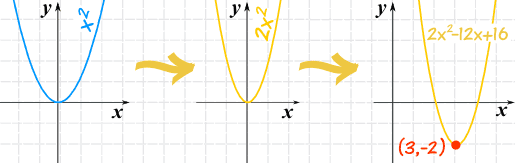



Graphing Quadratic Equations



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf
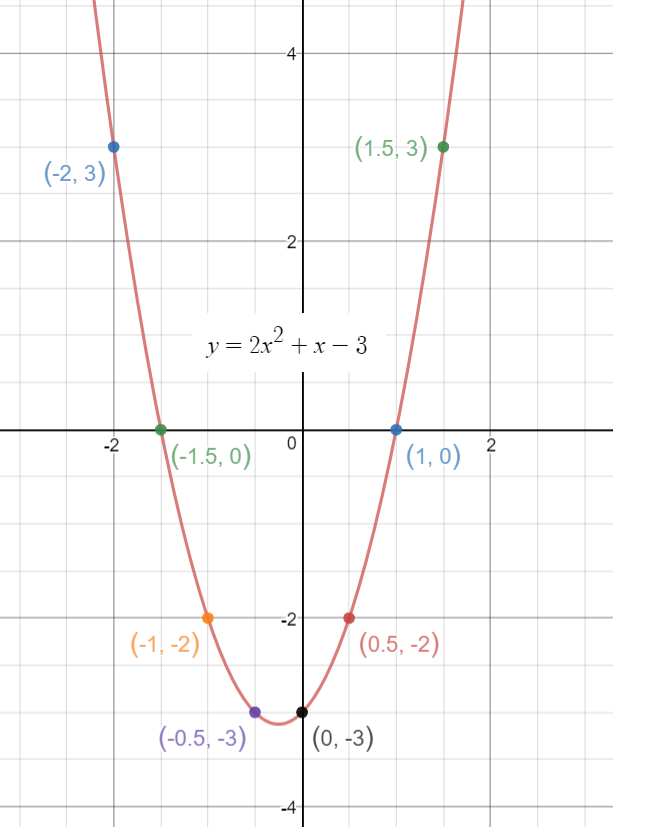



How To Do You Graph Y 2x 2 X 3 By Plotting Points Socratic
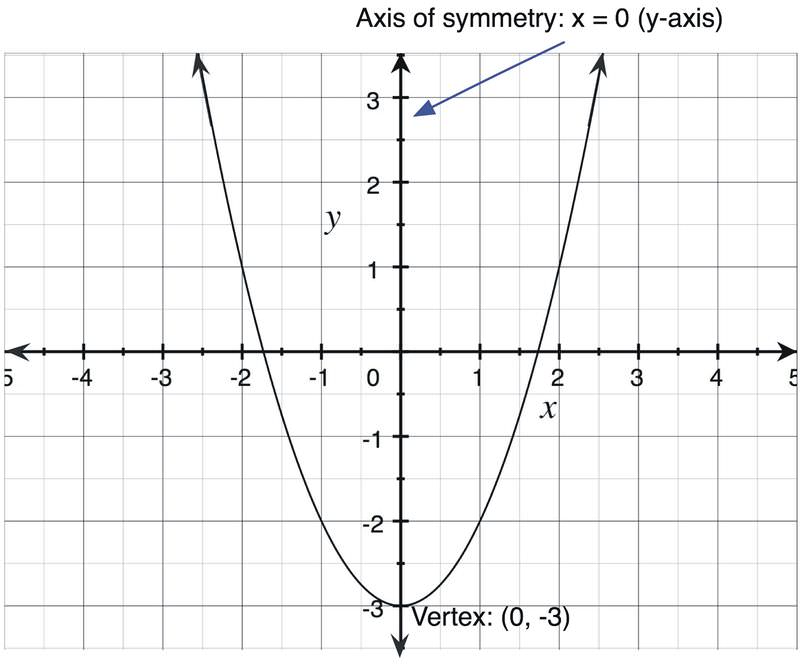



Square And Cube Function Families Read Algebra Ck 12 Foundation



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Quadratic Graphs Parabolas Ppt Download




A Quadratic Function F Is Given F X X2 2x 3 Chegg Com




Quadratic Function



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Group work 59 63 solutions Pdf




Fireworks From Standard To Vertex Form Ppt Video Online Download



How To Graph Y 2x 3 Youtube
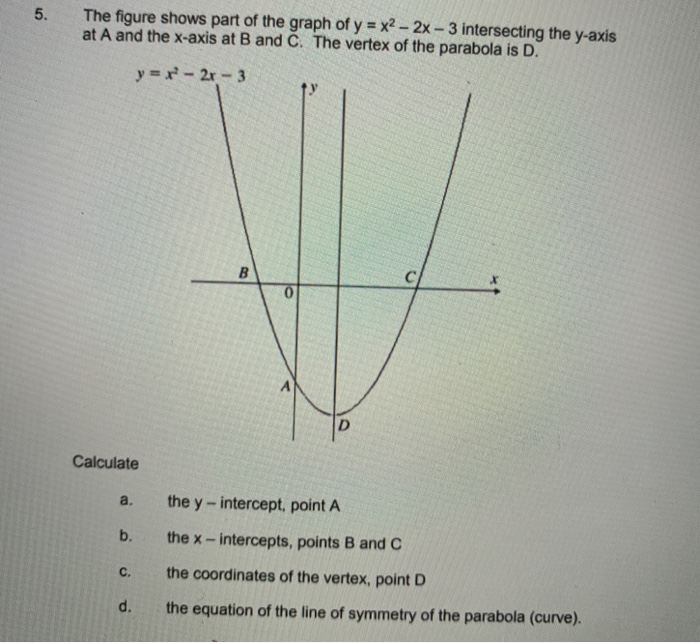



5 The Figure Shows Part Of The Graph Of Y X2 2x Chegg Com




Evaluate The Following Find The Domain And Range Chegg Com



Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x



0 件のコメント:
コメントを投稿