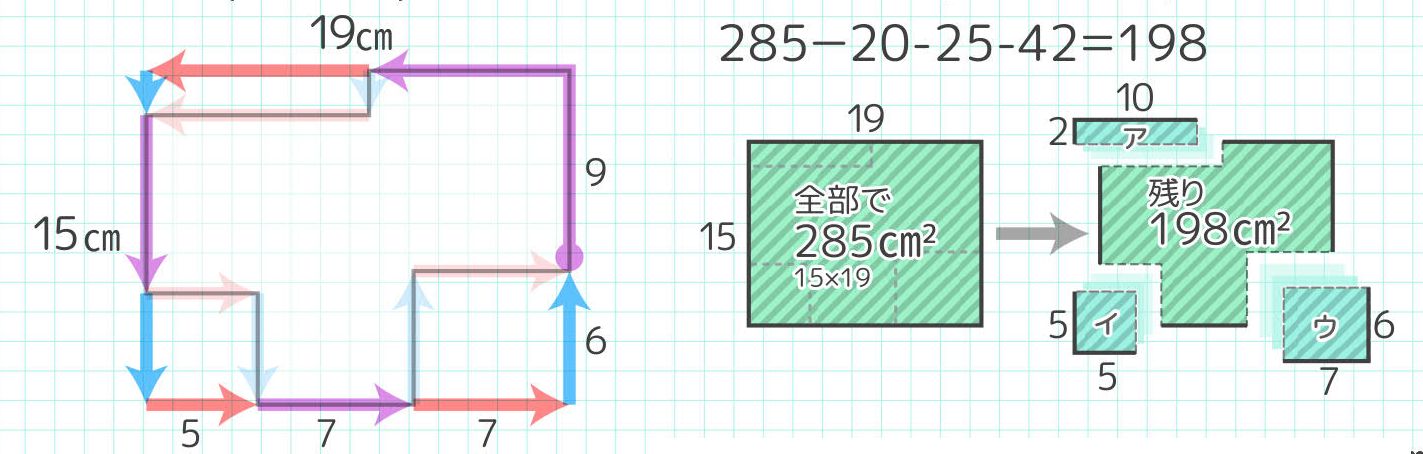
5秒後に直角三角形ABCと正方形DEFGが重なる部分の面積を求めなさい。 → 解答 (問題6) 対角線の長さが8cmの正方形を1つの頂点を中心に図のように45°回転させました。黒くぬった部分の面積を求めなさい。円周率は314とします。 → 解答314×36= 314×49= 314×64=096 314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから)
Math Battle 0274 4分円4個の重なり部分の面積
正方形 円 重なる 面積
正方形 円 重なる 面積-ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積4個分、または円が 2個分になるので、 12×314×2 =7536cm。 (2) 求める面積は円が 2個と正三角形2個 になる。 正六角形は正三角 形を6個あわせた ものなので、1個分 の面積は 9342÷6=1557。 求める面積は 6×6×314×2 +1557×2 =cm 2 。



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
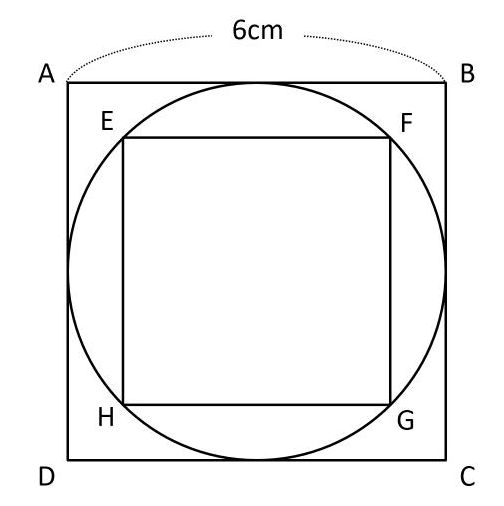
1辺2cmの正方形ABCDのそれぞれの頂点を中心として、半径2cmの円を4つ描くと、そのすべての円が重なる部分があります。 その面積は何c㎡になりますか? (小数第2位) ただし、円周率は3.14とし、1辺2cmの正三角形の面積は1.73c㎡とします。 参考イメージ図と面積計算 スマートホンアプリ「立方体の余弦定理など使わず、 3元1次連立方程式を解いて青の部分の面積を求める方法がありますよ。 下の図解で a が青の部分です。 ① a 4*b 4*c = 400 (正方形全体) ② a 3*b 2*c = 100*pi (4分円) ③ a 2*b c = 「60°の扇形」*2 三角形 「60°の扇形」*2 三角形 「正方形 円 面積」に関するQ&A: 正方形に円が重なる面積の問題です。 「円の面積の求め方」に関するQ&A: 円の面積の求め方 「situmon」に関するQ&A: noutihou no situmon desu
円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるかを考え,下のように円の面積の見当をつけます。 つまり,円の面積は半径を1辺とする正方形の面積の2倍と4倍の問題 P 単位正方形 U=0,1^{2} に含まれる半径が等しく,重ならない n 個の円の最大半径を求めよ この問題は,次の等価な問題に置き換えることができる 問題 Q 単位正方形 U 内の点対間の最小距離を最大化するような, n 個の点の位置を求めよ正八角形の対角線で囲まれた面積 東海中 08 円内を転がる正方形 雙葉中 07・6 転がる正方形 清真学園中 06・後期・3 長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中 16・第1日・9 転がる正方形 駒場東邦中 16・3
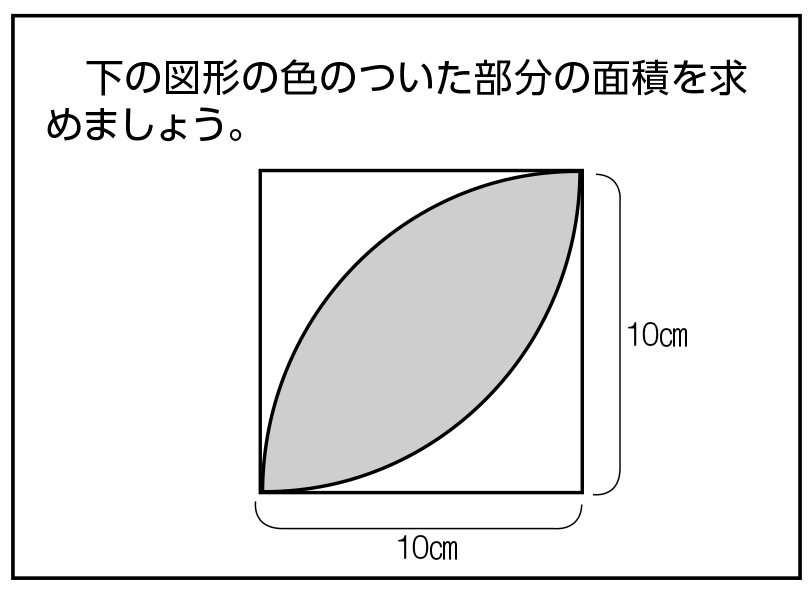
10cm*10cmの正方形があり、それぞれ4つの角を中心とする円が重なり合った部分の面積 *********************** 彼女のために3時まで考える南里さん とってもステキな方ですね!小さな正方形になる、ピッタリ重なるから、半分の面積だ。 答え 32c㎡ 考え方2 中の正方形の4分の1の面積をもとめ、その4倍をすれば良い。 4分の1の三角形の、たてと横のながさは、4cm だから が小さな三角形で その4倍が正方形だから 扇形と正方形重なる部分の面積はいくらか? 解 答 と置くと、 別 答 求める面積は、 次の式から求めることができます。 扇形CABの面積 + 扇形DBAの面積 - 正方形ADBCの面積 したがって、 求める面積




解き方と答えを教えてください Clear



中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー
第1問 色々な大きさの円 図形ドリル 第274問 四角形の面積 図形ドリル 第112問 正方形と半円 図形ドリル 第44問 直角二等辺三角形を折り返す 図形ドリル 第300問 長方形と面積円の面積学習における学習の流れ (子ども の音符の流れ)を次のように考えた。 ① 円の面積は円周内部の面に存在し,円 の半径と依存関係にあることに気づく。 ② 円の面積は,その円の半径を一辺とす る正方形の面積の2倍より大きく4倍よ図のように小さい円の半分を回転させると,凸の部分がちょうど凹の部分に重なるから,大きい円の面積の半分を求めるとよい (む) ※ 次の問題は中学一年生ではできませんが,中学卒業までにはできるように。 BDの長さは 4 次の図のように,1辺の長さがa (cm)の正方形ABCDを頂点Bを中心として45°回転したとき,辺BA,ADが通過する部分の面積 (cm 2) ヒント 黄色で



図形の移動 中学受験 田中貴 Com




正方形に内接する円と四分円に囲まれる面積 高校時代に友人から聞いて解けな Okwave
一辺の長さ $a$ の 正方形 (せいほうけい) の面積 $S$ は、次の公式で求められます。 正方形 (せいほうけい) の面積 \begin{align*} S = a^2 \end{align*} 面積 = 一辺 × 一辺入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイ・ 円積問題 ギリシア数学の三大難問の一つである円積問題は、 「与えられた円とちょうど等しい面積を持つ正方形を作図せよ。」 (コンパスと定木のみを使って) というものである。 同じ面積 ? 次の時間の予告 「円積問題ってどうやって解いたの?




正方形と内接する2つの4分の1円によってできる面積 小学5年生の娘から 数学 教えて Goo




重なり図形の面積計算 04ジュニア算数オリンピック Youtube
Z25 面積(重なる円) 円の半径はすべて10cmです。茶色の線で囲んだ部分の面積は何cm 2 ですか? 解答と解説 まだ発表していません。がんばってください! Z24 面積(不思議な結果があります) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい円の面積のおよその大きさを考えよう 半径10cmの円の外側に正方形を書くと → 上の図のように、円の面積は、1辺10cmの正方形4つ分の面積より小さいことに気づかせます。 円の外側の正方形の面積は、 (10×10)×4=400 です 半径10cm円は、その内側にあります。



下の図は 正方形と4つのおうぎ形を組み合わせたものです 正方形の1辺の長さ Yahoo 知恵袋




扇形と扇形が重なっている部分の面積の解き方を教えてください 円周率 中学校受験 教えて Goo
(1)正方形PQRSの面積は何cm2ですか。 (2)かげをつけた部分の面積の和は何cm2ですか。 <円とおうぎ形 面積その4> 右の図のように直径が重なった 2つの半円があ ります。小さい半円の中心はAで ,半径は 30cm, 大きい半円の中心はBで ,半径は40cmです。 本記事で考える円と正方形の位置関係 図1 本記事で考える円と正方形 本記事で考える円と正方形の位置関係は図1の通りです。正方形の一辺がその中点で円に外接している一方、その辺に属さない残りの頂点は円周上にあります。円とおうぎ形⑹ 弓形の面積 16 16 次の図は、1辺8㎝の正方形ABCDと、直径8㎝の円を4個組み合 わせた図形です。色のついた部分の面積を求めなさい。ただし円周率 は314とします。



Http Www Suguru Jp Pdf Yokude Yokude Php




長女の中学受験 算数の復習で最低限覚えておきたい図形 円と正方形の話を復習しました Pi Sukeのネットな生活
円、おうぎ形、木の葉形面積 これが中学入試に出た図形問題! 15年、神戸女学院中学部の出題問題より 円と正方形 15年、開成中学の面積問題から 15年、女子学院中学の求積問題より 15年(洛南高附属中学)影の部分の面積は? 15年(サレジオ学院36 面積1/nの正方形 先に芳賀の定理により、正方形の一辺をn等分することが可能であることが分かりました。すると、元の正方形の の面積の正方形をつくることができます.(n>1) 正三角形と円の重なり(白百合学園中学 14年) 網目部分の面積は?(城北中学 14年) 今年15年出題された問題から(四天王寺中学 15年) 15年、神戸女学院中学部の出題問題より 円と正方形
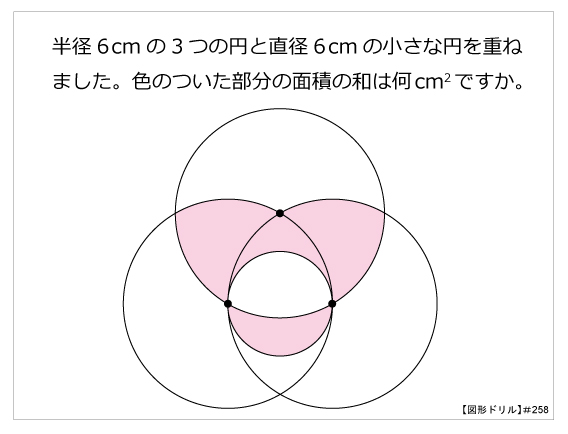



図形ドリル 第258問 円の重なり 算数星人のweb問題集 中学受験算数の問題に挑戦




ジュニア算数オリンピック 二次元上の面積を求める幾何の問題 円 ニート歴10年からの数学日記
第496回 合否を分ける問題の解き方 図形の回転移動 1 中学入試の合否を分ける問題について見ています。 前回までは、グラフの読み取りが大切な問題について考えてきましたが、今回からは 作図がポイントとなる問題 を取り扱っていこうと思います「ウの円の面積=エの円の面積」です。 「ケーキの法則」を使うと、「イの面積=カの面積」もわかります。 また、 から、 ウが(2)の「イの斜線部分の面積の1/2倍~」の答えになることがわかりますので、 ウと等しいア、エ、クも(2)の答えとわかります。求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形




面積の求め方 算数の教え上手 学びの場 Com



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S6 018teisei Pdf
大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え ㎠ 面積④ 重なりや移動でできた面積 例題5 長方形と正方形が下の図のように重なっています。色の付いた部分の面積を求めなさい。円に内接する面積最大の三角形 重なる部分の面積の最小 類題 ゴールキックで有利なのは・・・ 立体の切り口など 立方体の切り口 立方体の切り口の作図1 立方体の切り口の作図2 立方体の断面積の最小値 正四面体の切り口の円の面積は 8 2 9 2 d 2 {\displaystyle {\frac {8^ {2}} {9^ {2}}}d^ {2}} 、即ち 64 81 d 2 {\displaystyle {\frac {64} {81}}d^ {2}} だと記載されている 。 シュルバ・スートラ には インドの数学者 による近似の手法(精度は劣るが)が記録されている。 また、インドの数学者たちは与えられた正方形に対して、それに近い面積の円を近似的に作図する方法も与えている 。



並べ替えたら面積が変わっちまう 衝撃の理由がこちら 秒刊sunday




面白い数学の問題 半円の中の2つの正方形 証明までが解答です そらの暇つぶしch




正方形扇形面積 扇 おうぎ 形の面積を求める公式と弧の長さの求め方翻譯此網頁 Voajcr



正方形の中に四分円を2つ書いたもの 影の部分のまわりの長さはcm とい Yahoo 知恵袋



数学問題 一辺100mmの正方形で 半径100mmの円の4分の1の扇形が図のよ Yahoo 知恵袋



頭の体操 図形編




8 Ab A See How To Solve It At Qanda




円周角の新着記事 アメーバブログ アメブロ



小学校で習う知識だけで解けます ルートも使いません 東大生が小3のときに作った算数の問題 Togetter




解き方わかる方がいたら教えていただきたいです ちなみに答えは32p 64です Clear



4重の円の交わり 楽しいクイズの発信基地 クイズ大陸
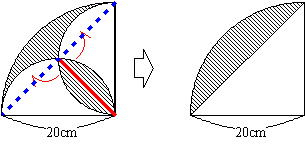



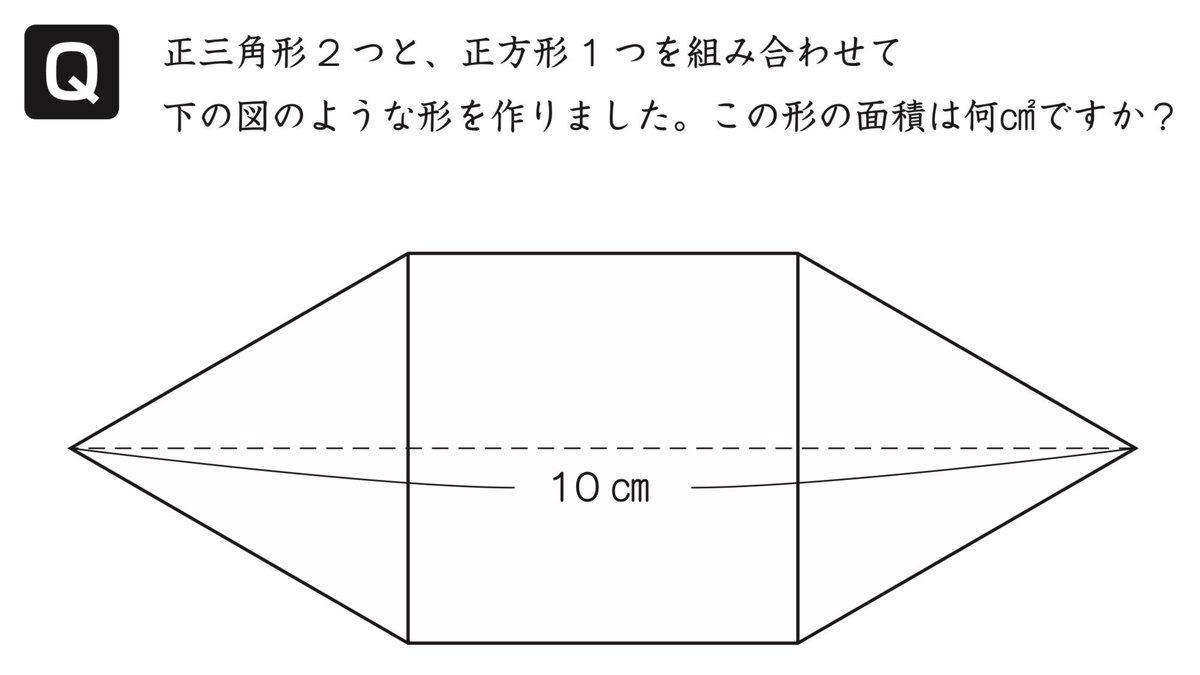
0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾
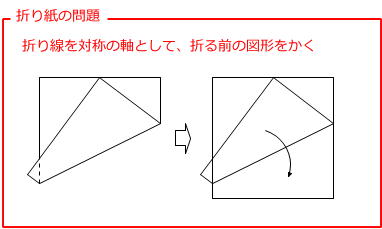



第512回 女子中の平面図形 2 前田昌宏の中学受験が楽しくなる算数塾



3図形が重なった部分の面積は 2004年ジュニア算数オリンピック トライアル問題より 算数オリンピック問題に挑戦



画像の2つの正方形を組み合わせてできた図形の重なってる部分の面積の求め Yahoo 知恵袋



ラグビーボールの重なり




Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 への道
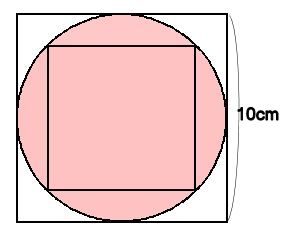



円の中の正方形



小2から プリント12枚 正方形長方形の面積の求め方と公式 対角線からも 中学受験まで そうちゃ式 受験算数 2号館 図形 速さ




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



扇形と正方形




円の面積 練習応用 Youtube



面積の求め方 算数の教え上手 学びの場 Com



Math 算数のコツ 18 円の中の正方形 働きアリ



超難問 ねこたさんのごった煮日和



Mondai67



面積の求め方 算数の教え上手 学びの場 Com



1



正方形 の 面積 の 求め 方 正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法 Amp Petmd Com



ファイル Bousi1 Jpg Wikipedia




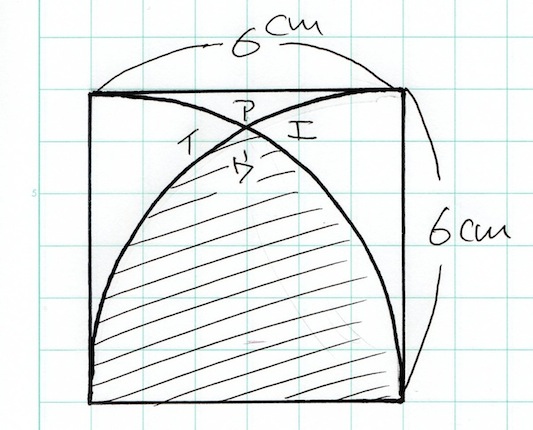
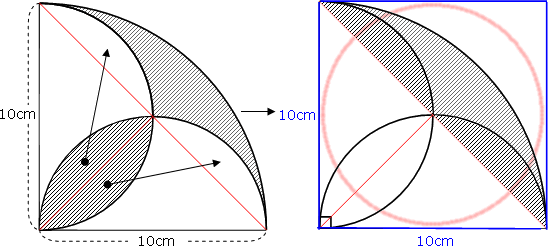
はっぱ型 の図形の面積 身勝手な主張




Asahi Com 朝日新聞社 面積の不思議 おーっ 花まる先生公開授業 教育
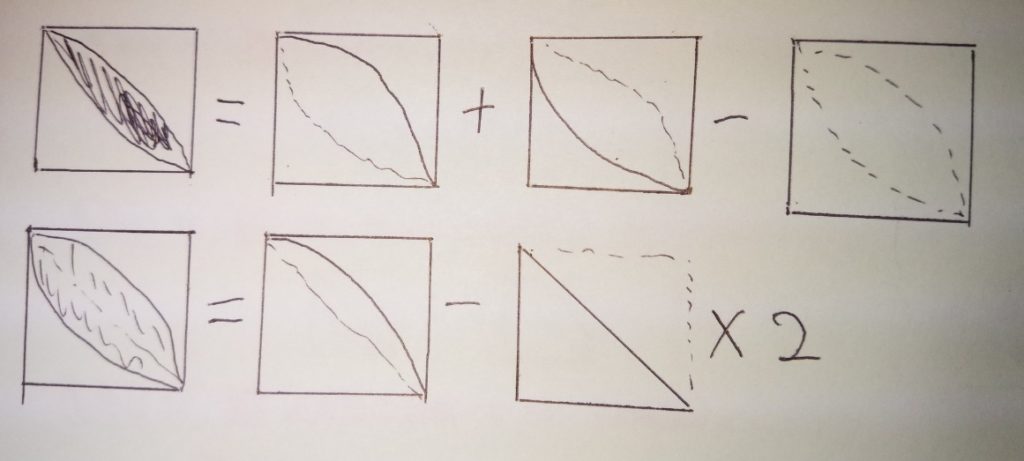



おうぎ形の面積の求め方2つと葉っぱ レンズ 形の面積の求め方3つ 等積移動 中学受験 塾なし の勉強法
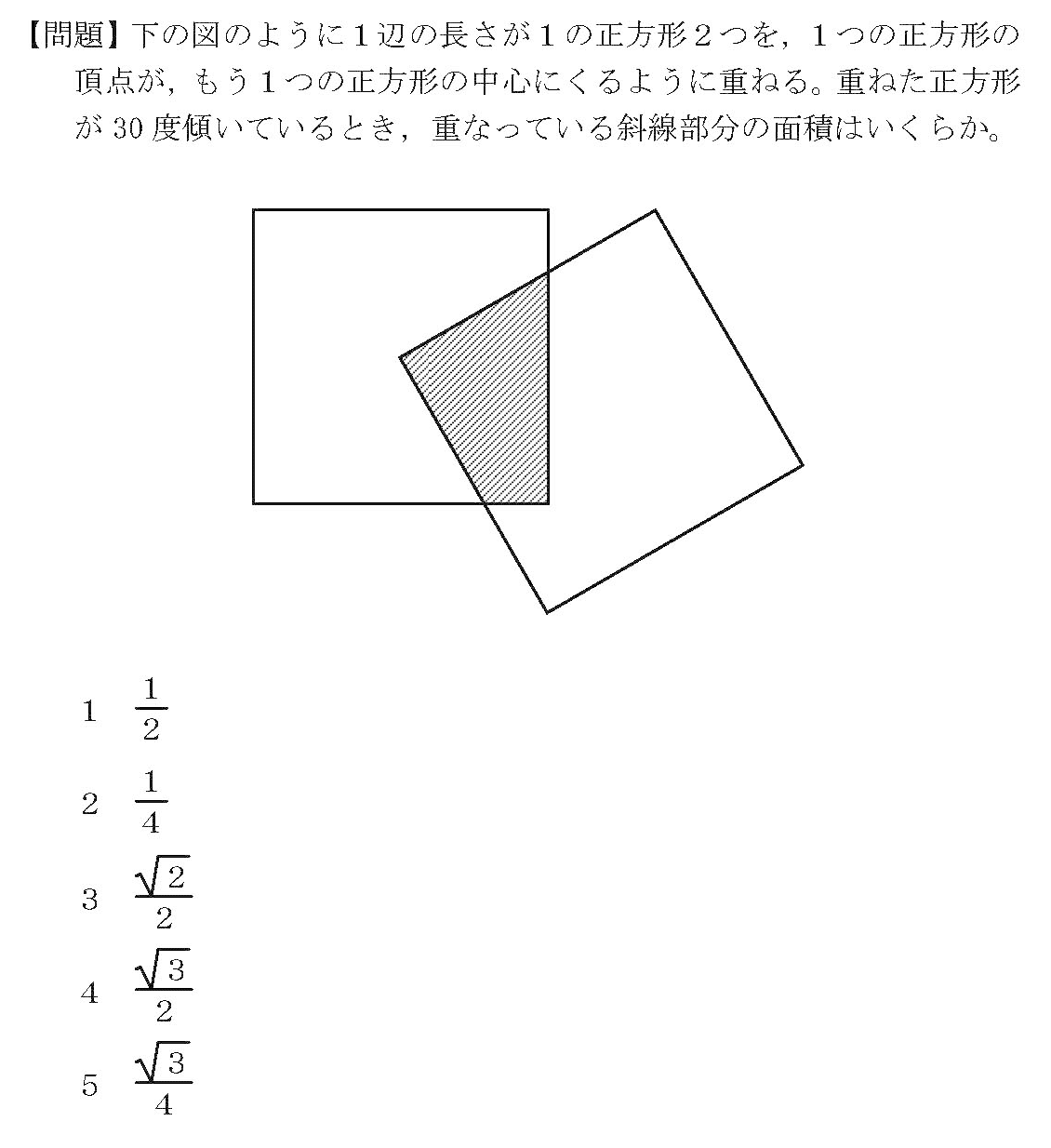



裁判所15 正方形の重なり 岡野朋一 Note



正方形とおうぎ形 奈良学園中学 算数入試問題 1998年 どう解く 中学受験算数




正方形と円で囲まれた図形の面積 おわり Takapの数学日記



図形を苦手にしない 小学生のうちに図形を得意にする方法 マナビコ Manabico



自作教材 円と扇形2 本質と技とコツ カテキョウブログ



File Bous2 Jpg Wikimedia Commons



Math Battle 0274 4分円4個の重なり部分の面積



円の中の正方形 基礎



1




標準 おうぎ形と正方形の面積 なかけんの数学ノート



正方形とおうぎ形 奈良学園中学 算数入試問題 1998年 どう解く 中学受験算数




正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



下の図は正方形の中に四分円と 半円を2つかいたものです 斜線部分の Yahoo 知恵袋



1




正方形 円 重なる 面積 の最高のコレクション 最高のぬりえ




小6 算数 小6 2 円の面積 応用編 Youtube




中学受験算数 まいにち算数172 重なりの面積 第16回算数オリンピックトライアル Youtube




正方形 算数星人のweb問題集 中学受験算数の問題に挑戦



1



4 12 半円の重なった部分の面積と周りの長さを求めるには さんすうがく



アタマを柔らかくする 脳トレ数学クイズ3選 リーダーシップ 教養 資格 スキル 東洋経済オンライン 社会をよくする経済ニュース



重なった正方形の面積 スクールプレゼンター教材共有サイト スクプレ道場



小6算数 円の面積 指導アイデア 2 みんなの教育技術



これで円の面積がわかるの 豊島岡女子学園中学 10年 イメージでわかる中学受験算数問題



面積を求める応用問題2 数学総復習
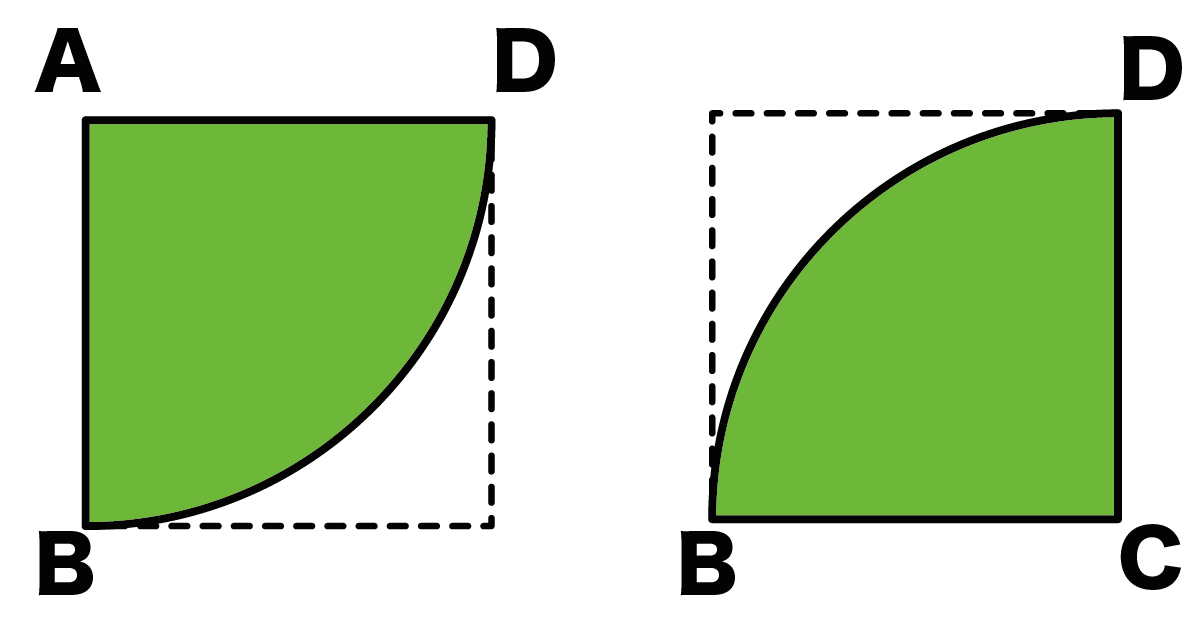



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



重なった3つの円の部分面積は 暁星中学 2014年 中学受験ー算数解き方ポータル
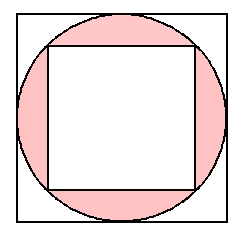



新着正方形 円 面積 最高のぬりえ



円積問題 Wikipedia



中学受験 0 57 葉状図形求積数




小5算数 おうぎ形の重なる面積 ブログ アビット



すぐるゼミ 図形の平行移動1



定期試験 実力試験 入学試験 直前チェック No 7




サレジオ 正方形を円の中に並べると ジーニアス 中学受験専門塾




斜線部の面積を計算してください これはクイズではありません マジで難 Okwave



小学6年生算数の問題です 問題 同じ正方形が2つ重なった部分の面 Yahoo 知恵袋



ラ サール11 5 図形の移動 正方形のまわりを長方形が1周する問題 気まぐれ解説カフェ 仮



Mondai67



立教新座11 1 の 3 平面図形 円の中に正方形が内接した図形 気まぐれ解説カフェ 仮



平面図形 中学受験ー算数解き方ポータル
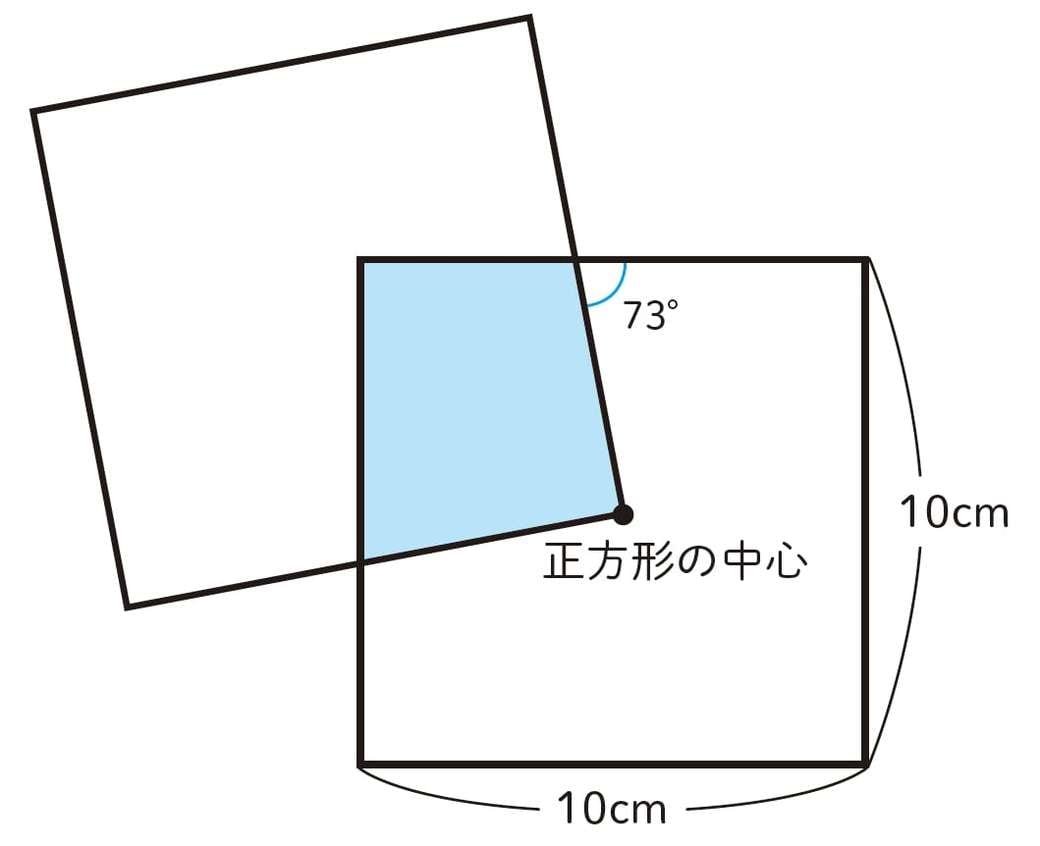



アタマを柔らかくする 脳トレ数学クイズ3選 リーダーシップ 教養 資格 スキル 東洋経済オンライン 社会をよくする経済ニュース
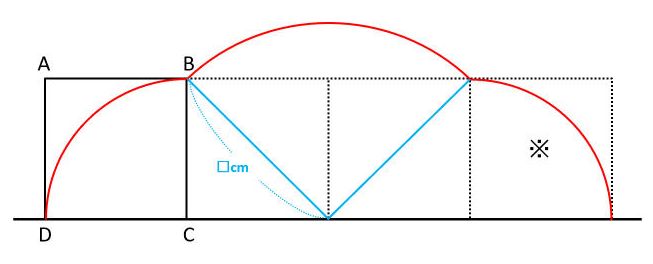



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




面積問題 9 桜蔭中 東久留米 学習塾 塾長ブログ




円の面積3 Final 算数



求積問題 正方形と扇形
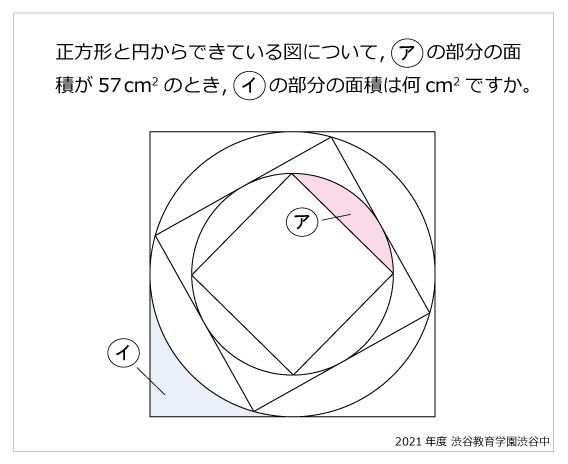



円 算数星人のweb問題集 中学受験算数の問題に挑戦
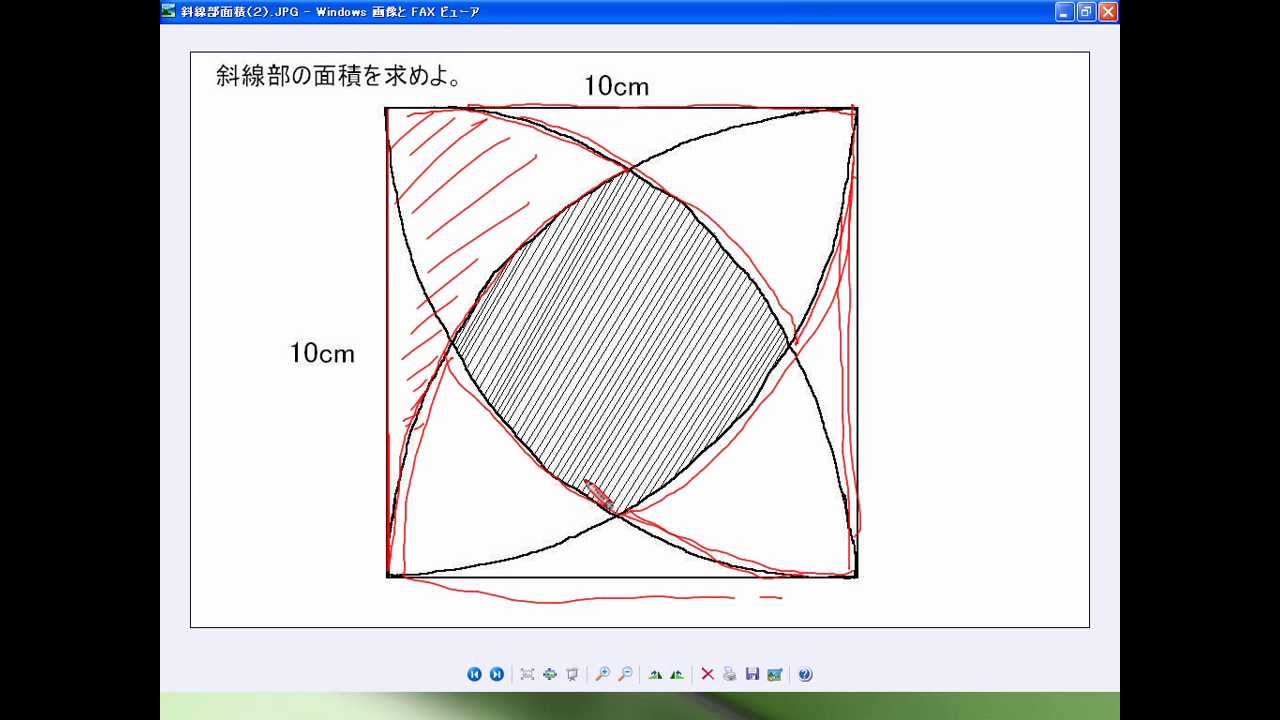



斜線部の面積 4 1辺10cmの正方形の場合 Youtube




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング




5つの円弧が重なる部分の面積 添付画像の図形についての問題です 正五角 Okwave



円 扇形 木の葉形面積 円が重なる部分の面積 1997 灘中 改題 これが中学入試に出た図形問題
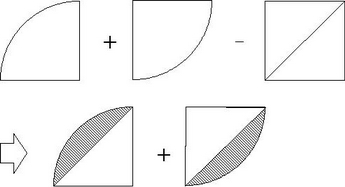



0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾
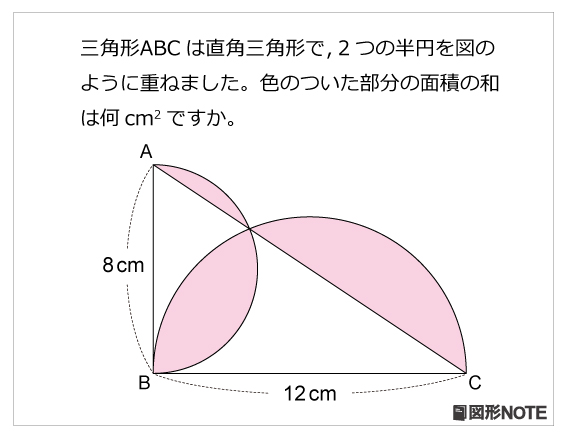



図形noteプレ レベル6 半円の重なり 算数星人のweb問題集 中学受験算数の問題に挑戦




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
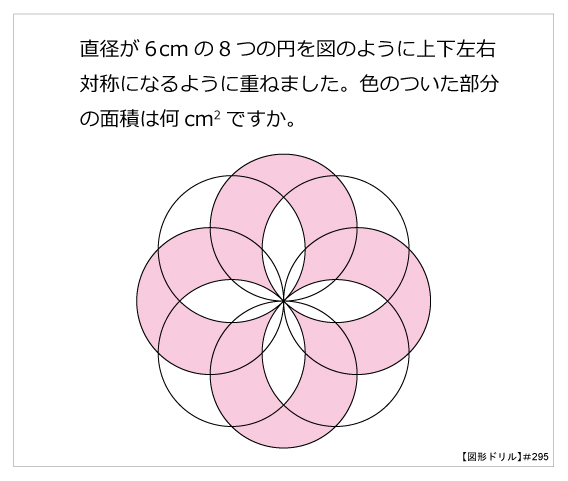



図形ドリル 第295問 8つの円の重なり 算数星人のweb問題集 中学受験算数の問題に挑戦




中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー




山と数学 そして英語 小学校算数 円の面積に関する応用問題



9th Stage 19 実は簡単に解ける 重なり合う5つの円の面積問題 数学クイズ なん度 Math Quiz Find Angles



0 件のコメント:
コメントを投稿